题目内容
11.函数$y={x^2}+\frac{1}{x}+1$在x=1处的切线方程是( )| A. | x-y+2=0 | B. | x-y-4=0 | C. | x+y-4=0 | D. | x+y+2=0 |
分析 求函数的导数,利用导数的几何意义即可求出切线方程.
解答 解:∵$y={x^2}+\frac{1}{x}+1$,
∴y′=2x-$\frac{1}{{x}^{2}}$,
x=1时,y′=1,
又x=1时,y=3,即切点坐标为(1,3),
则函数在x=1处的切线方程为y-3=x-1,
即x-y+2=0,
故选:A.
点评 本题主要考查导数的几何意义,根据导数和切线斜率之间的关系是解决本题的关键.

练习册系列答案
相关题目
2.圆(x-2)2+y2=4被直线x=1截得的弦长为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{3}$ |
19.已知向量$\overrightarrow a=(-1,0,2),\overrightarrow b=(1,1,0)$,且$\overrightarrow a+k\overrightarrow b与2\overrightarrow b-\overrightarrow a$相互垂直,则k值为( )
| A. | $\frac{7}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | 1 |
16.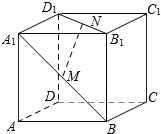 如图,在正方体ABCD-A1B1C1D1中,点M,N分别是面对角线A1B与B1D1的中点,若$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$,$\overrightarrow{D{D}_{1}}$=$\overrightarrow{c}$,则$\overrightarrow{MN}$=( )
如图,在正方体ABCD-A1B1C1D1中,点M,N分别是面对角线A1B与B1D1的中点,若$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$,$\overrightarrow{D{D}_{1}}$=$\overrightarrow{c}$,则$\overrightarrow{MN}$=( )
 如图,在正方体ABCD-A1B1C1D1中,点M,N分别是面对角线A1B与B1D1的中点,若$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$,$\overrightarrow{D{D}_{1}}$=$\overrightarrow{c}$,则$\overrightarrow{MN}$=( )
如图,在正方体ABCD-A1B1C1D1中,点M,N分别是面对角线A1B与B1D1的中点,若$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$,$\overrightarrow{D{D}_{1}}$=$\overrightarrow{c}$,则$\overrightarrow{MN}$=( )| A. | $\frac{1}{2}$($\overrightarrow{c}$+$\overrightarrow{b}$-$\overrightarrow{a}$) | B. | $\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$) | C. | $\frac{1}{2}$($\overrightarrow{a}$-$\overrightarrow{c}$) | D. | $\frac{1}{2}$($\overrightarrow{c}$-$\overrightarrow{a}$) |
3.函数$y={({\frac{1}{2}})^x}-2$的图象一定经过( )
| A. | 第一、二、三象限 | B. | 第一、二、四象限 | C. | 第一、三、四象限 | D. | 第二、三、四象限 |
20.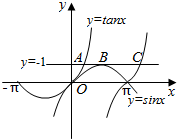 如图,已知A,B,C为直线y=1与函数y=sinx,y=tanx的图象在第一象限的三个相邻交点,若线段AC的长度记为|AC|,则|AB|:|BC|=( )
如图,已知A,B,C为直线y=1与函数y=sinx,y=tanx的图象在第一象限的三个相邻交点,若线段AC的长度记为|AC|,则|AB|:|BC|=( )
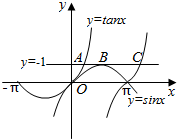 如图,已知A,B,C为直线y=1与函数y=sinx,y=tanx的图象在第一象限的三个相邻交点,若线段AC的长度记为|AC|,则|AB|:|BC|=( )
如图,已知A,B,C为直线y=1与函数y=sinx,y=tanx的图象在第一象限的三个相邻交点,若线段AC的长度记为|AC|,则|AB|:|BC|=( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:5 |