题目内容
11.已知数列{an}满足a1=1,$\frac{1}{{a}_{n+1}}$=$\sqrt{\frac{1}{{a}_{n}^{2}}+2}$,an>0,求an.分析 把已知的数列递推式两边平方,可得数列{$\frac{1}{{{a}_{n}}^{2}}$}是以2为公差的等差数列,求其通项公式后,取倒数再开方可得an.
解答 解:由$\frac{1}{{a}_{n+1}}$=$\sqrt{\frac{1}{{a}_{n}^{2}}+2}$,两边平方可得,$\frac{1}{{{a}_{n+1}}^{2}}=\frac{1}{{{a}_{n}}^{2}}+2$,
即$\frac{1}{{{a}_{n+1}}^{2}}-\frac{1}{{{a}_{n}}^{2}}=2$,
∴数列{$\frac{1}{{{a}_{n}}^{2}}$}是以2为公差的等差数列,
又a1=1,
∴$\frac{1}{{{a}_{n}}^{2}}=1+2(n-1)=2n-1$,
则${{a}_{n}}^{2}=\frac{1}{2n-1}$,
∵an>0,
∴an=$\sqrt{\frac{1}{2n-1}}$.
点评 本题考查数列递推式,考查了等差关系的确定,考查等差数列的通项公式的求法,是中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
1.已知a>0,b>0满足a+b=2,则$\frac{1}{a}+\frac{9}{b}$的最小值为( )
| A. | 4 | B. | 8 | C. | 16 | D. | 24 |
3.已知$\overrightarrow{a}$=(3,-1),$\overrightarrow{b}$=(1,-2),则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
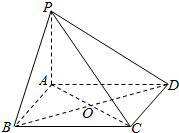 如图所示,PA垂直于正方形ABCD所在的平面,A为垂足,点O为正方形ABCD对角线AC和BD的交点.
如图所示,PA垂直于正方形ABCD所在的平面,A为垂足,点O为正方形ABCD对角线AC和BD的交点.