题目内容
15.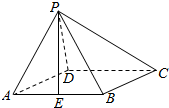 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.(Ⅰ)求证:CD∥平面PAB;
(Ⅱ)求证:PE⊥AD.
分析 (Ⅰ)由已知CD∥AB,由此能证明CD∥平面PAB.
(Ⅱ)推导出PE⊥AB,从而PE⊥平面ABCD,由此能证明PE⊥AD.
解答 证明:(Ⅰ)∵底面ABCD是菱形,
∴CD∥AB.(2分)
又∵CD?平面PAB,(4分)
且AB?平面PAB,
∴CD∥平面PAB.(5分)
(Ⅱ)∵PA=PB,点E是AB的中点,
∴PE⊥AB.(6分)
∵平面PAB⊥平面ABCD,
平面PAB∩平面ABCD=AB,PE?平面PAB,(8分)
∴PE⊥平面ABCD.(9分)
∵AD?平面ABCD,∴PE⊥AD.(10分)
点评 本题考查线面平行的证明,考查线线垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
3.函数$y={({\frac{1}{2}})^x}-2$的图象一定经过( )
| A. | 第一、二、三象限 | B. | 第一、二、四象限 | C. | 第一、三、四象限 | D. | 第二、三、四象限 |
10.定义在R上的偶函数f(x)满足f(x+2)=f(x),当x∈[-3,-2]时,f(x)=x2+4x+3,则y=f[f(x)]+1在区间[-3,3]上的零点个数为( )
| A. | 1个 | B. | 2个 | C. | 4个 | D. | 6个 |
20.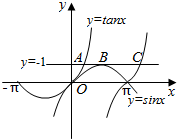 如图,已知A,B,C为直线y=1与函数y=sinx,y=tanx的图象在第一象限的三个相邻交点,若线段AC的长度记为|AC|,则|AB|:|BC|=( )
如图,已知A,B,C为直线y=1与函数y=sinx,y=tanx的图象在第一象限的三个相邻交点,若线段AC的长度记为|AC|,则|AB|:|BC|=( )
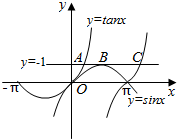 如图,已知A,B,C为直线y=1与函数y=sinx,y=tanx的图象在第一象限的三个相邻交点,若线段AC的长度记为|AC|,则|AB|:|BC|=( )
如图,已知A,B,C为直线y=1与函数y=sinx,y=tanx的图象在第一象限的三个相邻交点,若线段AC的长度记为|AC|,则|AB|:|BC|=( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:5 |
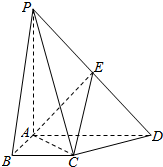 四棱锥P-ABCD的底面ABCD是直角梯形,∠DAB=∠ABC=90°,PA⊥底面ABCD,PA=AD=2,BC=AB=1,E为PD的中点.
四棱锥P-ABCD的底面ABCD是直角梯形,∠DAB=∠ABC=90°,PA⊥底面ABCD,PA=AD=2,BC=AB=1,E为PD的中点.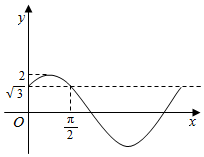 设函数f(x)=Asin(ωx+φ)(A,ω>0,0<|φ|<π)在一个周期内的图象如图所示.
设函数f(x)=Asin(ωx+φ)(A,ω>0,0<|φ|<π)在一个周期内的图象如图所示.