题目内容
16.某村投资128万元建起了一处生态采摘园,预计在经营过程中,第一年支出10万元,以后每年支出都比上一年增加4万元,从第一年起每年的销售收入都为76万元.设y表示前n(n∈N*)年的纯利润总和(利润总和=经营总收入-经营总支出-投资).(1)该生态园从第几年开始盈利?
(2)该生态园前几年的年平均利润最大,最大利润是多少?
分析 (1)每年的支出构成一个等差数列,每年的收入是一个常数列,故根据f利润总和=经营总收入-经营总支出-投资,可建立函数关系;
(2)求出年平均纯利润,再利用基本不等式,即可求得年平均纯利润的最大值.
解答 解:(1)依题意,每年支出组成首项为10,公差为4的等差数列,可得前n年的总支出10n+$\frac{n(n-1)}{2}$×4
可得前n(n∈N*)年的纯利润总和y=76n-[10n+$\frac{n(n-1)}{2}$×4]-128=-2n2+68n-128
由y>0,即-2n2+68n-128>0
解得2<n<32
由于n∈N+,故从第三年开始赢利.
(2)年平均纯利润$\frac{y}{n}$=-2n+68-$\frac{128}{n}$=68-2(n+$\frac{64}{n}$)≤36
当且仅当n=8时等号成立,此时年平均纯利润最大值为36万元,
即生态园前8年的年平均利润最大,最大利润是36万元.
点评 本题重点考查函数模型的构建,考查利用数学知识解决实际问题,考查利用基本不等式求函数的最值,解题的关键是寻找等量关系,建立函数关系式.

练习册系列答案
相关题目
11. 如图是某市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字,这些数据的中位数是( ),去掉一个最低分和最高分所剩数据的平均数是( )
如图是某市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字,这些数据的中位数是( ),去掉一个最低分和最高分所剩数据的平均数是( )
 如图是某市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字,这些数据的中位数是( ),去掉一个最低分和最高分所剩数据的平均数是( )
如图是某市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字,这些数据的中位数是( ),去掉一个最低分和最高分所剩数据的平均数是( )| A. | 86.5,86.7 | B. | 88,86.7 | C. | 88,86.8 | D. | 86,5,86.8 |
8.如图,某地区有7条南北向街道,5条东西街道,从A点走向B点最短的走法中,必须经过C点的概率( )
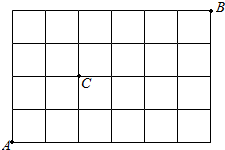

| A. | $\frac{3}{7}$ | B. | $\frac{6}{7}$ | C. | $\frac{3}{10}$ | D. | $\frac{7}{10}$ |
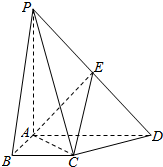 四棱锥P-ABCD的底面ABCD是直角梯形,∠DAB=∠ABC=90°,PA⊥底面ABCD,PA=AD=2,BC=AB=1,E为PD的中点.
四棱锥P-ABCD的底面ABCD是直角梯形,∠DAB=∠ABC=90°,PA⊥底面ABCD,PA=AD=2,BC=AB=1,E为PD的中点.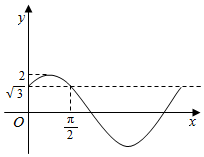 设函数f(x)=Asin(ωx+φ)(A,ω>0,0<|φ|<π)在一个周期内的图象如图所示.
设函数f(x)=Asin(ωx+φ)(A,ω>0,0<|φ|<π)在一个周期内的图象如图所示.