题目内容
1.已知函数f(x)=log2x,g(x)=x2+2x,数列{an}的前n项和记为Sn,bn为数列{bn}的通项,n∈N*.点(bn,n)和(n,Sn)分别在函数f(x)和g(x)的图象上.(1)求数列{an}和{bn}的通项公式;
(2)令Cn=$\frac{1}{{{a_n}•f({b_{2n-1}})}}$,求数列{Cn}的前n项和Tn.
分析 (1)由题意可得:n=log2bn,解得bn=2n.Sn=n2+2n,当n≥2时,an=Sn-Sn-1,即可得出an.
(2)f(b2n-1)=$lo{g}_{2}{2}^{2n-1}$=2n-1.可得Cn=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,利用“裂项求和”即可得出.
解答 解:(1)由题意可得:n=log2bn,解得bn=2n.
Sn=n2+2n,当n≥2时,Sn-1=(n-1)2+2(n-1),
∴an=Sn-Sn-1=2n+1.
当n=1时也成立,
∴an=2n+1.
(2)f(b2n-1)=$lo{g}_{2}{2}^{2n-1}$=2n-1.
Cn=$\frac{1}{{{a_n}•f({b_{2n-1}})}}$=$\frac{1}{(2n+1)(2n-1)}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,
∴数列{Cn}的前n项和Tn=$\frac{1}{2}[(1-\frac{1}{3})$+$(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{2n-1}-\frac{1}{2n+1})]$=$\frac{1}{2}(1-\frac{1}{2n+1})$=$\frac{n}{2n+1}$.
点评 本题考查了指数与对数的运算性质、数列的递推关系、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.若命题p是假命题,命题q是真命题,则( )
| A. | p∧q是真命题 | B. | p∨q是假命题 | C. | ?p是假命题 | D. | ¬q是假命题 |
16.如图,在平行六面体ABCD-A′B′C′D′中,若$\overrightarrow{AB}=\vec a$,$\overrightarrow{AD}=\overrightarrow b$,$\overrightarrow{AA'}=\overrightarrow c$,则$\overrightarrow{BM}$=( )
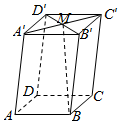

| A. | $-\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | B. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | C. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ | D. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ |
10.定义在R上的偶函数f(x)满足f(x+2)=f(x),当x∈[-3,-2]时,f(x)=x2+4x+3,则y=f[f(x)]+1在区间[-3,3]上的零点个数为( )
| A. | 1个 | B. | 2个 | C. | 4个 | D. | 6个 |
11. 如图是某市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字,这些数据的中位数是( ),去掉一个最低分和最高分所剩数据的平均数是( )
如图是某市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字,这些数据的中位数是( ),去掉一个最低分和最高分所剩数据的平均数是( )
 如图是某市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字,这些数据的中位数是( ),去掉一个最低分和最高分所剩数据的平均数是( )
如图是某市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字,这些数据的中位数是( ),去掉一个最低分和最高分所剩数据的平均数是( )| A. | 86.5,86.7 | B. | 88,86.7 | C. | 88,86.8 | D. | 86,5,86.8 |