题目内容
14.在空间直角坐标系中,点M(0,2,-1)和点N(-1,1,0)的距离是$\sqrt{3}$.分析 根据所给的两个点的坐标和空间中两点的距离公式,代入数据写出两点的距离公式,做出最简结果,不能再化简为止.
解答 解:∵点M(0,2,-1)和点N(-1,1,0),
∴|MN|=$\sqrt{{(0+1)}^{2}{+(2-1)}^{2}{+(-1-0)}^{2}}$=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题考查两点之间的距离公式的应用,是一个基础题,这种题目在计算时只要不把数据代入出现位置错误,就可以做出正确结果.

练习册系列答案
相关题目
2.圆(x-2)2+y2=4被直线x=1截得的弦长为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{3}$ |
9.若命题p是假命题,命题q是真命题,则( )
| A. | p∧q是真命题 | B. | p∨q是假命题 | C. | ?p是假命题 | D. | ¬q是假命题 |
19.已知向量$\overrightarrow a=(-1,0,2),\overrightarrow b=(1,1,0)$,且$\overrightarrow a+k\overrightarrow b与2\overrightarrow b-\overrightarrow a$相互垂直,则k值为( )
| A. | $\frac{7}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | 1 |
3.函数$y={({\frac{1}{2}})^x}-2$的图象一定经过( )
| A. | 第一、二、三象限 | B. | 第一、二、四象限 | C. | 第一、三、四象限 | D. | 第二、三、四象限 |
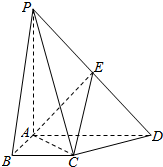 四棱锥P-ABCD的底面ABCD是直角梯形,∠DAB=∠ABC=90°,PA⊥底面ABCD,PA=AD=2,BC=AB=1,E为PD的中点.
四棱锥P-ABCD的底面ABCD是直角梯形,∠DAB=∠ABC=90°,PA⊥底面ABCD,PA=AD=2,BC=AB=1,E为PD的中点.