题目内容
18.已知$\overrightarrow{a}$=(1,-3,1),$\overrightarrow{b}$=(-1,1,-3),则|$\overrightarrow{a}$-$\overrightarrow{b}$|=6.分析 根据空间向量的坐标运算,求出$\overrightarrow{a}$-$\overrightarrow{b}$,再求它的模长.
解答 解:∵$\overrightarrow{a}$=(1,-3,1),$\overrightarrow{b}$=(-1,1,-3),
∴$\overrightarrow{a}$-$\overrightarrow{b}$=(2,-4,4),
∴|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{{2}^{2}{+(-4)}^{2}{+4}^{2}}$=6.
故答案为:6.
点评 本题考查了空间向量的坐标运算与求模长的应用问题,是基础题目.

练习册系列答案
相关题目
3.已知$\overrightarrow{a}$=(3,-1),$\overrightarrow{b}$=(1,-2),则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
9.若命题p是假命题,命题q是真命题,则( )
| A. | p∧q是真命题 | B. | p∨q是假命题 | C. | ?p是假命题 | D. | ¬q是假命题 |
3.函数$y={({\frac{1}{2}})^x}-2$的图象一定经过( )
| A. | 第一、二、三象限 | B. | 第一、二、四象限 | C. | 第一、三、四象限 | D. | 第二、三、四象限 |
10.定义在R上的偶函数f(x)满足f(x+2)=f(x),当x∈[-3,-2]时,f(x)=x2+4x+3,则y=f[f(x)]+1在区间[-3,3]上的零点个数为( )
| A. | 1个 | B. | 2个 | C. | 4个 | D. | 6个 |
8.如图,某地区有7条南北向街道,5条东西街道,从A点走向B点最短的走法中,必须经过C点的概率( )
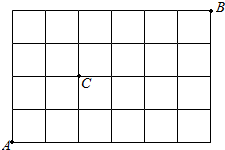

| A. | $\frac{3}{7}$ | B. | $\frac{6}{7}$ | C. | $\frac{3}{10}$ | D. | $\frac{7}{10}$ |