题目内容
1.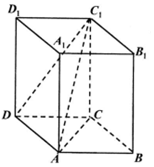 如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC=$\sqrt{3}$,BC=BB1=2.
如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC=$\sqrt{3}$,BC=BB1=2.(Ⅰ)求证:AC⊥平面ABB1A1;
(Ⅱ)求二面角A-C1D-C的平面角的余弦值.
分析 (Ⅰ)推导出AB⊥AC,AA1⊥AC,由此能证明AC⊥平面ABB1A1.
(Ⅱ)过点C作CP⊥C1D于P,连接AP,则AC⊥平面DCC1D1,从而∠CPA是二面角A-C1D-C的平面角,由此能求出二面角A-C1D-C的平面角的余弦值.
解答 证明:(Ⅰ)∵在底面ABCD中,AB=1,AC=$\sqrt{3}$,BC=2,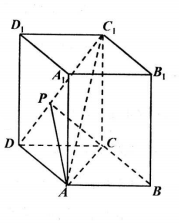
∴AB2+AC2=BC2,∴AB⊥AC,
∵侧棱AA1⊥底面ABCD,∴AA1⊥AC,
又∵AA1∩AB=A,AA1,AB?平面ABB1A1,
∴AC⊥平面ABB1A1.
解:(Ⅱ)过点C作CP⊥C1D于P,连接AP,
由(Ⅰ)可知,AC⊥平面DCC1D1,
∠CPA是二面角A-C1D-C的平面角,
∵CC1=BB1=2,CD=AB=1,∴CP=$\frac{DC×C{C}_{1}}{D{C}_{1}}$=$\frac{1×2}{\sqrt{1+4}}$=$\frac{2\sqrt{5}}{5}$,
∴tan$∠CPA=\frac{AC}{CP}$=$\frac{\sqrt{15}}{2}$,∴cos$∠CPA=\frac{2\sqrt{19}}{19}$,
∴二面角A-C1D-C的平面角的余弦值为$\frac{2\sqrt{19}}{19}$.
点评 本题考查线面垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
12.甲乙和其他4名同学合影留念,站成两排三列,且甲乙两人不在同一排也不在同一列,则这6名同学的站队方法有( )
| A. | 144种 | B. | 180种 | C. | 288种 | D. | 360种 |
9.设Sn为等差数列{an}的前n项和,若$\frac{{S}_{1}}{{S}_{4}}$=$\frac{1}{10}$,则$\frac{{S}_{3}}{{S}_{5}}$=( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
16.已知随机变量ξ的分布列如下:
则E(ξ)的最小值为$\frac{3}{4}$,此时b=$\frac{1}{2}$.
| ξ | 0 | 1 | 2 |
| P | b | a2 | $\frac{1}{2}$-$\frac{a}{2}$ |
6.函数f(x)=3sin(2x-$\frac{π}{3}$)的图象可以由y=3sin2x的图象( )
| A. | 向右平移$\frac{π}{3}$个单位长度得到 | B. | 向左平移$\frac{π}{3}$个单位长度得到 | ||
| C. | 向右平移$\frac{π}{6}$个单位长度得到 | D. | 向左平移$\frac{π}{6}$个单位长度得到 |
10. 私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成如表:
私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成如表:
(Ⅰ)完成被调查人员的频率分布直方图;
(Ⅱ)若从年龄在[55,65),的被调查者中各随机选取2人进行追踪调查,记选中的2人中赞成“车辆限行”的人数为X,求随机变量X的分布列和数学期望.
 私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成如表:
私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成如表:| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(Ⅱ)若从年龄在[55,65),的被调查者中各随机选取2人进行追踪调查,记选中的2人中赞成“车辆限行”的人数为X,求随机变量X的分布列和数学期望.
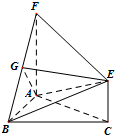 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF${\;}_{=}^{∥}$2CE,G是线段BF上一点,AB=AF=BC
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF${\;}_{=}^{∥}$2CE,G是线段BF上一点,AB=AF=BC