题目内容

10．已知M={y|y=2x+3，x∈R}，N={y|y=-x2+2x+6，x∈R}，M∩N=（3，7]．

分析 根据函数的性质求出集合的等价条件，根据集合的基本运算进行求解即可．

解答 解：由y=2x+3＞3，得M=（3，+∞），
由y=-x2+2x+6=-（x-1）2+7≤7，
即N=（-∞，7]，
则M∩N=（3，7]，
故答案为：（3，7]

点评 本题主要考查集合的基本运算，根据函数的性质求出集合的等价条件是解决本题的关键．

练习册系列答案
相关题目
20．已知，若f（x）=$\left\{\begin{array}{l}{x+2（x≤-1）}\\{{x}^{2}（-1＜x＜2）}\\{2x（x≥2）}\end{array}\right.$，则函数的值域是R．
1．若sinα+sinβ=$\frac{1}{4}$，cosα+cosβ=$\frac{1}{3}$，求cos（α-β）的值．
18．求一条直线经过点A（2，-3），并且它的斜率等于直线$\sqrt{3}$y-x=0的斜率的直线方程．
5．数列{an}的前n项和为$\frac{1}{1+2+3+…+n}$，则数列{an}的前n项和为$\frac{2n}{n+1}$．
15．设函数f（2x+1）=${3}^{4{x}^{2}+2x}$，则f（1）=（　　）
A．0B．1C．3D．36
4．等差数列{an}有无穷多项，其前n项和为Sn，已知$\frac{{S}_{3}}{3}$+$\frac{{S}_{4}}{4}$+$\frac{{S}_{5}}{5}$=27，$\frac{{S}_{3}}{3}$×$\frac{{S}_{4}}{4}$×$\frac{{S}_{5}}{5}$=693．
（1）数列{an}的通项an；
（2）是否存在n，使得$\frac{{S}_{n}}{n}$+$\frac{128}{n+1}$取得最小值，如果存在，求出n的值，如果不存在，请说明理由．
1．101110（2）转化为十进制数是46．
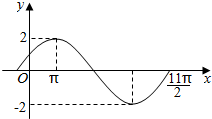2．已知函数$f（x）=Asin（ωx+\frac{π}{6}）（A＞0，ω＞0）$）图象的一部分如图所示．
（1）求函数f（x）的解析式；
（2）设$α，β∈[\frac{π}{2}，π]，f（3α-\frac{π}{2}）=\frac{10}{13}，f（3β+π）=-\frac{6}{5}$，求cos（α-β）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网