题目内容
18．求一条直线经过点A（2，-3），并且它的斜率等于直线$\sqrt{3}$y-x=0的斜率的直线方程．分析 求出所求直线的斜率，利用点斜式，即可求得方程．
解答 解：直线$\sqrt{3}$y-x=0的斜率为$\frac{\sqrt{3}}{3}$
∵所求直线的斜率等于直线$\sqrt{3}$y-x=0的斜率、
∵直线经过点A（2，-3），
∴直线的方程是y+3=$\frac{\sqrt{3}}{3}$（x-2），即x-$\sqrt{3}$y-2-3$\sqrt{3}$=0
所求直线方程为：x-$\sqrt{3}$y-2-3$\sqrt{3}$=0．
点评 本题考查直线方程，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
8．一个几何体的三视图如图所示，则该几何体的表面积为（ ）
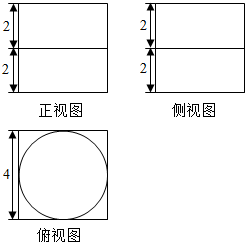
| A． | 64+8π | B． | 48+12π | C． | 48+8π | D． | 48+12π |
13．已知Sn是数列{an}的前n项和，若Sn=1-an，则数列{an}是（ ）
| A． | 等差数列 | B． | 递减的等比数列 | C． | 递增的等比数列 | D． | 不是等比数列 |
3．函数f（x）=2sin（ωx+$\frac{π}{4}$）（ω＞0）与函数g（x）=cos（ωx+φ）（|φ|＜$\frac{π}{2}$）的对称轴完全相同，则φ=（ ）
| A． | -$\frac{π}{4}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{2}$ | D． | -$\frac{π}{2}$ |
10．
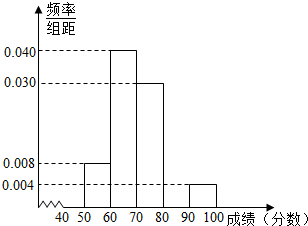学校从参加高二年级期末考试的学生中抽出一些学生，并统计了他们的数学成绩（成绩均为整数且满分为100分），所得数据整理后，列出了如下频率分布表．
（Ⅰ）在给出的样本频率分布表中，求A，B，C的值；
（Ⅱ）补全频率分布直方图，并利用它估计全体高二年级学生期末数学成绩的众数、中位数；
（Ⅲ）现从分数在[80，90），[90，100]的9名同学中随机抽取两名同学，求被抽取的两名学生分数均不低于90分的概率．
学校从参加高二年级期末考试的学生中抽出一些学生，并统计了他们的数学成绩（成绩均为整数且满分为100分），所得数据整理后，列出了如下频率分布表．（Ⅰ）在给出的样本频率分布表中，求A，B，C的值；
（Ⅱ）补全频率分布直方图，并利用它估计全体高二年级学生期末数学成绩的众数、中位数；
| 分组 | 频数 | 频率 |
| [40，50） | A | 0.04 |
| [50，60） | 4 | 0.08 |
| [60，70） | 20 | 0.40 |
| [70，80） | 15 | 0.30 |
| [80，90） | 7 | B |
| [90，100] | 2 | 0.04 |
| 合计 | C | 1 |