题目内容
5.数列{an}的前n项和为$\frac{1}{1+2+3+…+n}$,则数列{an}的前n项和为$\frac{2n}{n+1}$.分析 求出an的表达式,利用裂项消项法求解数列的前n项和.
解答 解:由题意得,an=$\frac{1}{1+2+3+…+n}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n+1}$),
所以数列{an}的前n项和Sn=2[(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{4}$)+…+($\frac{1}{n}$-$\frac{1}{n+1}$)]
=2(1-$\frac{1}{n+1}$)=$\frac{2n}{n+1}$,
故答案为:$\frac{2n}{n+1}$
点评 本题考查裂项相消法求数列的前n项和,注意解题的规律.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
16. 如图所示,当参数λ分别取λ1,λ2时,函数f(x)=$\frac{x}{2-λx}$(x≥0)的部分图象分别对应曲线C1,C2,则有( )
如图所示,当参数λ分别取λ1,λ2时,函数f(x)=$\frac{x}{2-λx}$(x≥0)的部分图象分别对应曲线C1,C2,则有( )
 如图所示,当参数λ分别取λ1,λ2时,函数f(x)=$\frac{x}{2-λx}$(x≥0)的部分图象分别对应曲线C1,C2,则有( )
如图所示,当参数λ分别取λ1,λ2时,函数f(x)=$\frac{x}{2-λx}$(x≥0)的部分图象分别对应曲线C1,C2,则有( )| A. | 0<λ1<λ2 | B. | 0<λ2<λ1 | C. | λ1<λ2<0 | D. | λ2<λ1<0 |
13.已知Sn是数列{an}的前n项和,若Sn=1-an,则数列{an}是( )
| A. | 等差数列 | B. | 递减的等比数列 | C. | 递增的等比数列 | D. | 不是等比数列 |
20.已知lga+lgb=lg2,$\frac{a}{{a}^{2}+2}$+$\frac{b}{{b}^{2}+2}$的最大值是( )
| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
17.已知$y=\sqrt{2016}$,则y′=( )
| A. | $\frac{1}{{2\sqrt{2016}}}$ | B. | $-\frac{1}{{2\sqrt{2016}}}$ | C. | $\frac{2016}{{\sqrt{2016}}}$ | D. | 0 |
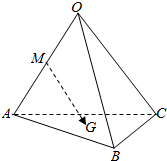 如图所示,已知空间四边形OABC,其对角线为OB,AC,M是边OA的中点,G是△ABC的重心,用基向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$表示向量$\overrightarrow{MG}$的表达式为$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$-$\frac{1}{6}$$\overrightarrow{OA}$.
如图所示,已知空间四边形OABC,其对角线为OB,AC,M是边OA的中点,G是△ABC的重心,用基向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$表示向量$\overrightarrow{MG}$的表达式为$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$-$\frac{1}{6}$$\overrightarrow{OA}$.