题目内容
△ABC的三个内角A,B,C所对的边分别为a,b,c,已知b=3且角A,B,C依次成等差数列,
(Ⅰ)若边a,b,c依次成等比数列,求△ABC的面积;
(Ⅱ)求△ABC周长的取值范围.
(Ⅰ)若边a,b,c依次成等比数列,求△ABC的面积;
(Ⅱ)求△ABC周长的取值范围.
考点:等差数列与等比数列的综合
专题:综合题,等差数列与等比数列,解三角形
分析:(Ⅰ)先利用等差中项的定义求出B,利用边a,b,c依次成等比数列,求出ac,再利用三角形面积公式求解;
(Ⅱ)先由正弦定理用角A、B表示出a、b,实现了边向角的转变,进而转化成三角函数求值域问题求解.
(Ⅱ)先由正弦定理用角A、B表示出a、b,实现了边向角的转变,进而转化成三角函数求值域问题求解.
解答:
解:(Ⅰ)∵三内角A、B、C的度数成等差数列,
∴2B=A+C,
∵A+B+C=180°,
∴B=60°,
∵a、b、c成等比数列,∴b2=ac,
∵b=3,
∴S=
acsinB=
;
(Ⅱ)根据正弦定理,可得△ABC周长y=a+3+c=2
sinA+2
sinC+3=6sin(B+30°)+3,
∵0<B<120°,
∴
<sin(B+30°)≤1,
∴6<6sin(B+30°)+3≤9,
∴△ABC周长的取值范围为(6,9].
∴2B=A+C,
∵A+B+C=180°,
∴B=60°,
∵a、b、c成等比数列,∴b2=ac,
∵b=3,
∴S=
| 1 |
| 2 |
9
| ||
| 4 |
(Ⅱ)根据正弦定理,可得△ABC周长y=a+3+c=2
| 3 |
| 3 |
∵0<B<120°,
∴
| 1 |
| 2 |
∴6<6sin(B+30°)+3≤9,
∴△ABC周长的取值范围为(6,9].
点评:本题综合考查了数列和三角函数以及解三角形的有关知识,考查了学生的分析能力和运算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某城市有3个演习点同时进行消防演习,现将4个消防队分配到这3个演习点,若每个演习点至少安排1个消防队,则不同的分配方案种数位( )
| A、12 | B、36 | C、72 | D、108 |
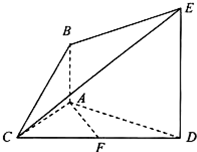 如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=4,DE=2AB=3,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=4,DE=2AB=3,且F是CD的中点.
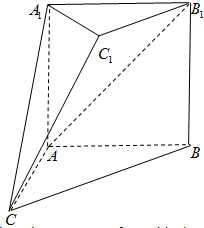 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,