题目内容
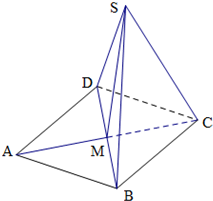 菱形ABCD中,∠BAD=60°,AB=4,且AC∩BD=M,现将三角形BD沿着BD折起形成四面体SBCD,如图所示.
菱形ABCD中,∠BAD=60°,AB=4,且AC∩BD=M,现将三角形BD沿着BD折起形成四面体SBCD,如图所示.(Ⅰ)当∠SMC为多大时,SM⊥面BCD?并证明;
(Ⅱ)在(Ⅰ)的条件下,求点D到面SBC的距离.
考点:点、线、面间的距离计算,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)当∠SMC=90°时,利用线面垂直的判定定理证明SM⊥面BCD;
(Ⅱ)设点D到面SBC的距离为d,由等体积法可得:VS-DBC=VD-SBC,即可得出结论.
(Ⅱ)设点D到面SBC的距离为d,由等体积法可得:VS-DBC=VD-SBC,即可得出结论.
解答:
 解:(Ⅰ)当∠SMC=90°时,SM⊥面BCD.
解:(Ⅰ)当∠SMC=90°时,SM⊥面BCD.
证明:此时SM⊥CM,且由条件SM⊥BD,
CM,BD为面BCD内两条相交直线,所以SM⊥面BCD;
(Ⅱ)设点D到面SBC的距离为d,则
在(Ⅰ)的条件下,有SC=2
,而SB=BC=4,
所以三角形SBC的面积为2
,
由等体积法可得:VS-DBC=VD-SBC,
∴
•2
•d=
•4
•2
,
∴d=
.
 解:(Ⅰ)当∠SMC=90°时,SM⊥面BCD.
解:(Ⅰ)当∠SMC=90°时,SM⊥面BCD.证明:此时SM⊥CM,且由条件SM⊥BD,
CM,BD为面BCD内两条相交直线,所以SM⊥面BCD;
(Ⅱ)设点D到面SBC的距离为d,则
在(Ⅰ)的条件下,有SC=2
| 6 |
所以三角形SBC的面积为2
| 15 |
由等体积法可得:VS-DBC=VD-SBC,
∴
| 1 |
| 3 |
| 15 |
| 1 |
| 3 |
| 3 |
| 3 |
∴d=
4
| ||
| 5 |
点评:本题考查直线与平面垂直的判定,考查等体积法,考查学生分析解决问题的能力,难度中等.

练习册系列答案
相关题目
已知椭圆:
+
=1(a,b>0)和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B.若椭圆上存在点P,使得
•
=0,则椭圆离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| PA |
| PB |
A、[
| ||||||
B、(0,
| ||||||
C、[
| ||||||
D、[
|
已知等比数列{an}的各项均为正数,公比q≠1,设P=
(log0.5a4+log0.5a8),Q=log0.5
,则P与Q的大小关系是( )
| 1 |
| 2 |
| a2+a10 |
| 2 |
| A、P≥Q | B、P<Q |
| C、P≤Q | D、P>Q |