题目内容
如果一个几何体的三视图如图所示（单位长度：cm），则此几何体的体积是（ ）A、
| ||
| B、64 | ||
C、
| ||
D、
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：几何体是正方体与正四棱锥的组合体，判断正方体的棱长与正四棱锥的底面边长及高，把数据代入正方体与棱锥的体积公式计算．
解答：
解：由三视图知：几何体是正方体与正四棱锥的组合体，
其中正方体的棱长与正四棱锥的底面边长都是4，四棱锥的高为2．
∴几何体的体积V=43+
×42×2=64+
=
（cm3）．
故选：C．
其中正方体的棱长与正四棱锥的底面边长都是4，四棱锥的高为2．
∴几何体的体积V=43+
| 1 |
| 3 |
| 32 |
| 3 |
| 224 |
| 3 |
故选：C．
点评：本题考查了由三视图求几何体的体积，根据三视图判断几何体的形状及数据所对应的几何量是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
复数（
）3的共轭复数为（ ）
| 1+i |
| 1-i |
| A、1 | B、-1 | C、i | D、-i |
设n∈N*，曲线y=xn（1-x）在x=2处的切线与y轴交点的纵坐标为an，则a4为（ ）
| A、80 | B、32 |
| C、192 | D、256 |
设a，b是两条不同直线，α，β是两个不同平面，下列四个命题中正确的是（ ）
| A、若a，b与α所成的角相等，则a∥b |
| B、若a∥α，b∥β，α∥β，则a∥b |
| C、若a⊥α，b⊥β，α⊥β，则a⊥b |
| D、若a?α，b?β，a∥b，则α∥β |
已知复数a+bi=
（a、b∈R），则z=b+（a-1）i在复平面上对应的点位于（ ）
| 2+i |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
二项式（2
-
）6的展开式的常数项是（ ）
| x |
| 1 | ||
2
|
| A、20 | B、-20 |
| C、15 | D、-15 |
i是虚数单位，
的共轭复数为（ ）
| 2i |
| 1-i |
| A、-1+i | B、1+i |
| C、-1-i | D、1-i |
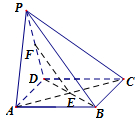如图，已知四棱锥P-ABCD的底面为菱形，对角线AC与BD相交于点E，平面PAC垂直于底面ABCD，线段PD的中点为F．