题目内容
10.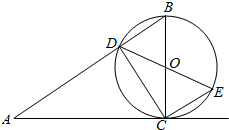 如图,BC是圆O的直径,过C作圆O的切线AC,连接AB交圆O于点D.
如图,BC是圆O的直径,过C作圆O的切线AC,连接AB交圆O于点D.(Ⅰ)若AC=3,圆O的半径为1,求AD;
(Ⅱ)连接DO并延长交圆O于点E,连接CE,求证:CD2=AD•CE.
分析 (Ⅰ)由切割线定理,可得AD;
(Ⅱ)利用射影定理,结合△OBD≌△OCE,证明:CD2=AD•CE.
解答 (Ⅰ)解:由题意,BC⊥AC,BC=2,AC=3,∴AB=$\sqrt{13}$,
由切割线定理,可得9=AD•AB,∴AD=$\frac{9\sqrt{13}}{13}$;
(Ⅱ)证明:∵BC是圆O的直径,
∴CD⊥AB,
∴CD2=AD•BD,
∵△OBD≌△OCE,
∴BD=CE,
∴CD2=AD•CE.
点评 本题考查切割线定理,射影定理,△OBD≌△OCE,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.已知集合A={1,2,m},B={3,4}.若A∩B={3},则实数m=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.已知函数f(x)的图象如图所示,则f(x)的解析式可能是( )
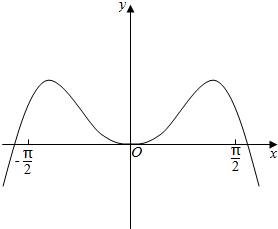

| A. | x2cosx | B. | sinx2 | C. | xsinx | D. | x2-$\frac{1}{6}$x4 |
19.设一直棱柱的底面是边长为2$\sqrt{2}$正方形,棱柱的顶点都在同一个球面上,且这个球面的表面积为64π,则该四棱柱的对角线与底面成的角是( )
| A. | 30° | B. | 38° | C. | 45° | D. | 60° |
 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点,设AC中点为O.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点,设AC中点为O.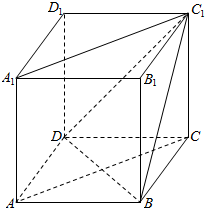 如图,在正方体ABCD-A1B1C1D1中,求直线BC1与AC的夹角60°.
如图,在正方体ABCD-A1B1C1D1中,求直线BC1与AC的夹角60°.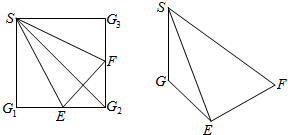 如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体S-EFG中.
如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体S-EFG中.