题目内容
5.单调递增的等差数列{an},a2=1,且a2,a3,a6成等比数列.(1)求数列{an}的通项公式;
(2)若{an} 的前n 项和为Sn,设bn=$\frac{1}{{S}_{n+2}}$,求数列{bn} 的前n 项和Tn.
分析 (1)设单调递增的等差数列{an}的公差为d,运用等比数列的中项性质,结合等差数列的通项公式,即可得到所求;
(2)运用等差数列的求和公式,可得bn=$\frac{1}{{S}_{n+2}}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),再由数列的求和方法:裂项相消求和,化简即可得到所求和.
解答 解:(1)设单调递增的等差数列{an}的公差为d,
由a2=1,且a2,a3,a6成等比数列,
可得a32=a2a6,即有(1+d)2=1•(1+4d),
解得d=2(0舍去),
则an=a2+(n-2)d=1+2(n-2)=2n-3;
(2)由(1)可得a1=-1,d=2,
可得Sn=na1+$\frac{1}{2}$n(n-1)d=n(n-2),
即有bn=$\frac{1}{{S}_{n+2}}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),
前n 项和Tn=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+…+$\frac{1}{n-1}$-$\frac{1}{n+1}$+$\frac{1}{n}$-$\frac{1}{n+2}$)
=$\frac{1}{2}$(1+$\frac{1}{2}$--$\frac{1}{n+1}$-$\frac{1}{n+2}$)
=$\frac{3{n}^{2}+5n}{4{n}^{2}+12n+8}$.
点评 本题考查等差数列的通项公式和求和公式的运用,考查等比数列的中项的性质,同时考查数列的求和方法:裂项相消求和,考查化简运算能力,属于中档题.

| A. | y=x与y=($\sqrt{x}$)2 | B. | y=x与|x| | ||
| C. | y=x2-1与y=t2-1 | D. | y=2x-1,x∈Z与y=2x+1,x∈Z |
| A. | 1 | B. | $\frac{3}{2}$ | C. | 3 | D. | 6 |

 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点,设AC中点为O.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点,设AC中点为O. 如图,底面ABCD为矩形,侧棱PA⊥底面ABCD,$AB=\sqrt{3}$,BC=1,PA=2,求直线AC与PB所成角的余弦值.
如图,底面ABCD为矩形,侧棱PA⊥底面ABCD,$AB=\sqrt{3}$,BC=1,PA=2,求直线AC与PB所成角的余弦值.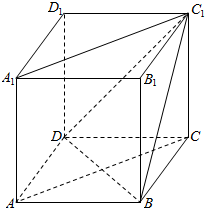 如图,在正方体ABCD-A1B1C1D1中,求直线BC1与AC的夹角60°.
如图,在正方体ABCD-A1B1C1D1中,求直线BC1与AC的夹角60°.