题目内容
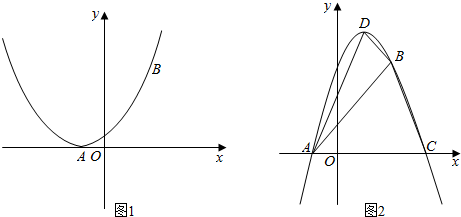
7.设函数f(x)=|(a+1)x+2|.(1)当a=0时,画出函数y=f(x)的图象;
(2)当a>0时,求方程|(a+1)x+2|=|x+1|+|ax+1|的解集.
分析 (1)当a=0时,f(x)=|x+2|,从而作出其图象;
(2)化简可得|ax+1+x+1|=|x+1|+|ax+1|,从而化为(x+1)•(ax+1)≥0,从而分类讨论解得.
解答  解:(1)当a=0时,f(x)=|x+2|,从而作其图象如图,
解:(1)当a=0时,f(x)=|x+2|,从而作其图象如图,
(2)∵|(a+1)x+2|=|x+1|+|ax+1|,
∴|ax+1+x+1|=|x+1|+|ax+1|,
∴(x+1)•(ax+1)≥0,
①当0<a<1时,-$\frac{1}{a}$<-1,
∴原不等式的解集为(-∞,-$\frac{1}{a}$]∪[-1,+∞);
②当a=1时,原不等式的解集为R;
③当a>1时,-$\frac{1}{a}$>-1,
∴原不等式的解集为(-∞,-1]∪[-$\frac{1}{a}$,+∞).
点评 本题考查了函数的化简与绝对值函数的图象的作法,同时考查了绝对值性质的应用及分类讨论的思想应用,化简为(x+1)•(ax+1)≥0是关键.

练习册系列答案
相关题目
19.设一直棱柱的底面是边长为2$\sqrt{2}$正方形,棱柱的顶点都在同一个球面上,且这个球面的表面积为64π,则该四棱柱的对角线与底面成的角是( )
| A. | 30° | B. | 38° | C. | 45° | D. | 60° |
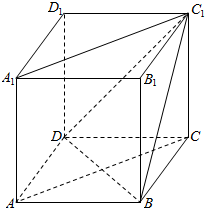 如图,在正方体ABCD-A1B1C1D1中,求直线BC1与AC的夹角60°.
如图,在正方体ABCD-A1B1C1D1中,求直线BC1与AC的夹角60°.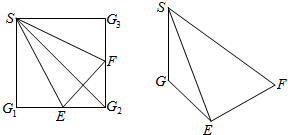 如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体S-EFG中.
如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体S-EFG中.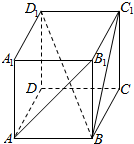 如图,在正方体ABCD-A1B1C1D1中.求:
如图,在正方体ABCD-A1B1C1D1中.求: