题目内容
15.已知数列{an}满足a1=9,其前n项和为Sn,对n∈N*,n≥2,都有Sn=3(Sn-1-2)(Ⅰ)求数列{an}的通项;
(Ⅱ)求证:数列{Sn+$\frac{9}{2}$}是等比数列;
(Ⅲ)若bn=-2log3an+20,n∈N*,求数列{bn}的前n项和Tn的最大值.
分析 (Ⅰ)由Sn=3(Sn-1-3),Sn+1=3(Sn-3),相减可得an+1=3an.利用等比数列的通项公式即可得出.
(Ⅱ)利用等比数列的前n项和公式可得Sn,变形即可得出.
(Ⅲ)由(Ⅰ)可知bn=-2log3an+20=-2n+18,利用等差数列的前n项和公式,二次函数的单调性即可得出.
解答 解:(Ⅰ)∵Sn=3(Sn-1-3),Sn+1=3(Sn-3),
∴an+1=3an.
故{an}是公比为3,首项为9的等比数列,${a_n}={3^{n+1}}$,
(Ⅱ)∵${a_n}=9•{3^{n-1}}$,
∴${S_n}=\frac{{9(1-{3^n})}}{1-3}=-\frac{9}{2}+\frac{9}{2}•{3^n}$,
∴${S_n}+\frac{9}{2}=\frac{9}{2}•{3^n}=\frac{27}{2}•{3^{n-1}}$,${S_1}+\frac{9}{2}=\frac{9}{2}•3=\frac{27}{2},\;\;\frac{{{S_{n+1}}+\frac{9}{2}}}{{{S_n}+\frac{9}{2}}}=\frac{{\frac{27}{2}{3^n}}}{{\frac{27}{2}{3^{n-1}}}}=3$.
故数列$\left\{{{S_n}+\frac{9}{2}}\right\}$是$\frac{27}{2}$为首项,公比为3的等比数列.
(Ⅲ)由(Ⅰ)可知bn=-2log3an+20=-2n+18,
∴{bn}是公差为-2.首项为16的等差数列.
∴${T_n}=-{n^2}+17n$,
∵b8>0,b9=0,b10<0,
∴T8或T9最大,最大值为72.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、二次函数的单调性、递推关系的应用,考查了推理能力与计算能力,属于中档题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
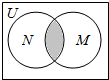 已知全集U=R,集合M={x|-1≤x≤3}和集合N={x|x=2k-1,k∈N}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合为( )
已知全集U=R,集合M={x|-1≤x≤3}和集合N={x|x=2k-1,k∈N}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合为( )| A. | {x|-1≤x≤3} | B. | {-3,-1,1,3,5} | C. | {-1,1,3} | D. | {-1,1,3,5} |
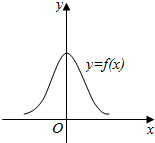
| A. | f(x)=e${\;}^{1-{x}^{2}}$ | B. | f(x)=e${\;}^{{x}^{2}-1}$ | C. | f(x)=e${\;}^{{x}^{2}}$-1 | D. | f(x)=ln(x2-1) |
 某几何体的三视图如图所示,其俯视图的外轮廓是由一个半圆与其直径组成的图形,则此几何体的体积是$\frac{8π}{3}$.
某几何体的三视图如图所示,其俯视图的外轮廓是由一个半圆与其直径组成的图形,则此几何体的体积是$\frac{8π}{3}$.