题目内容
5.函数f(x)=32x-a•3x+2,若x>0时,f(x)≥0恒成立,则实数a的取值范围是(-∞,2$\sqrt{2}$].分析 设t=3x(t>1),即有t2-at+2≥0在t>1恒成立,即为a≤t+$\frac{2}{t}$的最小值,运用基本不等式可得最小值,即可得到a的范围.
解答 解:设t=3x(t>1),即有t2-at+2≥0在t>1恒成立,
即为a≤t+$\frac{2}{t}$的最小值,
由t+$\frac{2}{t}$≥2$\sqrt{t•\frac{2}{t}}$=2$\sqrt{2}$,当且仅当t=$\sqrt{2}$,即x=log3$\sqrt{2}$时,取得最小值.
即有a≤2$\sqrt{2}$,
故答案为:(-∞,2$\sqrt{2}$].
点评 本题考查不等式恒成立问题的解法,注意运用换元法转化为二次不等式恒成立问题,运用参数分离和基本不等式,考查运算能力,属于中档题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
16.已知集合M={-1,0,1,2,3}和N={x|x=2k-1,k∈N},则M∩N=( )
| A. | {x|-1≤x≤3} | B. | {-3,-1,1,3,5} | C. | {-1,1,3} | D. | {-1,1,3,5} |
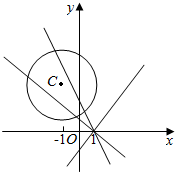 已知圆C的方程为(x+1)2+(y-3)2=4,过点(1,0)的直线l的斜率为k,设圆C上到l的距离为l的点的个数z,求z关于k的函数关系式.
已知圆C的方程为(x+1)2+(y-3)2=4,过点(1,0)的直线l的斜率为k,设圆C上到l的距离为l的点的个数z,求z关于k的函数关系式.