题目内容
7.已知函数f(x)的图象如图所示,则f(x)的解析式可能是( )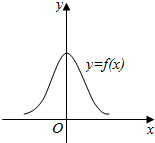
| A. | f(x)=e${\;}^{1-{x}^{2}}$ | B. | f(x)=e${\;}^{{x}^{2}-1}$ | C. | f(x)=e${\;}^{{x}^{2}}$-1 | D. | f(x)=ln(x2-1) |
分析 结合函数的图象,利用函数的定义域,最值以及单调性进行判断即可.
解答 解:函数关于y轴对称,则函数f(x)为偶函数.
f(0)有意义,则排除D.若f(x)=ln(x2-1),则f(0)=ln(-1)无意义,不满足条件.
f(0)>0,p排除C,若f(x)=e${\;}^{{x}^{2}}$-1,则f(0)=1-1=0,不满足条件.
当x=0时,函数f(x)取得最大值,排除B,
故选:A
点评 本题主要考查函数解析式的判断,利用函数图象的性质,利用排除法是解决本题的关键.

练习册系列答案
相关题目
17.已知一个几何体的三视图如图所示,则该几何体的体积为( )


| A. | 4π | B. | 3π | C. | 2π | D. | π |
19.在△ABC中,若AB=4,BC=5,B=60°,则AC=( )
| A. | $\sqrt{21}$ | B. | $\sqrt{31}$ | C. | $\sqrt{51}$ | D. | $\sqrt{61}$ |
16.已知集合M={-1,0,1,2,3}和N={x|x=2k-1,k∈N},则M∩N=( )
| A. | {x|-1≤x≤3} | B. | {-3,-1,1,3,5} | C. | {-1,1,3} | D. | {-1,1,3,5} |
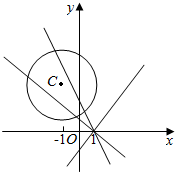 已知圆C的方程为(x+1)2+(y-3)2=4,过点(1,0)的直线l的斜率为k,设圆C上到l的距离为l的点的个数z,求z关于k的函数关系式.
已知圆C的方程为(x+1)2+(y-3)2=4,过点(1,0)的直线l的斜率为k,设圆C上到l的距离为l的点的个数z,求z关于k的函数关系式.