题目内容
已知函数f(x)=x2-ax+a.设p:方程f(x)=0有实数根;q:函数f(x)在区间[1,2]上是增函数.若p和q有且只有一个正确,求实数a的取值范围.
考点:命题的真假判断与应用
专题:简易逻辑
分析:首先考虑命题p,q均为真命题,求出a的取值范围,再根据p,q中一真一假,分别求出a的取值范围,最后求并集.
解答:
解:若p真,即方程f(x)=0有实数根,
则△=a2-4a≥0?a≤0,或a≥4;…(2分)
若q真,即函数f(x)在区间[1,2]上是增函数,
则区间[1,2]在对称轴的右边即
≤1⇒a≤2…(3分)
因为p和q有且只有一个正确,所以p,q中一真一假.
若p真q假,则
⇒a≥4;
若p假q真,则
⇒0<a≤2.…(7分)
所以实数a的取值范围为(0,2]∪[4,+∞)…(8分)
则△=a2-4a≥0?a≤0,或a≥4;…(2分)
若q真,即函数f(x)在区间[1,2]上是增函数,
则区间[1,2]在对称轴的右边即
| a |
| 2 |
因为p和q有且只有一个正确,所以p,q中一真一假.
若p真q假,则
|
若p假q真,则
|
所以实数a的取值范围为(0,2]∪[4,+∞)…(8分)
点评:本题主要考查命题的真假判断和应用,同时考查函数的单调性和集合、不等式的运算,是一道基础题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
在△ABC中,A=30°,a=
,b=2,则此三角形解的情况是( )
| 2 |
| A、一解 | B、两解 |
| C、无数个解 | D、不存在 |
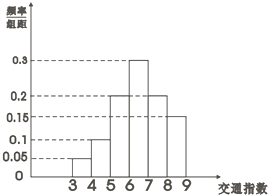 交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵,晚高峰时段,从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制直方图如图所示.
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵,晚高峰时段,从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制直方图如图所示.