题目内容
f(x)=lg
,其中a是实数,n是任意给定的正自然数且n≥2,如果f(x)当x∈(-∞,1]时有意义,求a的取值范围.
| 1+2x+3x+…+(n-1)x+nxa |
| n |
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:分离参数a>-[(
)x+(
)x+…+(
)x],运用函数y=(
)x,k=1,2,3…n-1,在(-∞,1]上都是增函数
,y=-[(
)x+(
)x+…+(
)x],(-∞,1]上也是增函数,求解最值问题即可.
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| k |
| n |
,y=-[(
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
解答:
解:f(x)当x∈(-∞,1]时有意义的条件是1+2x+…+(n-1)x+nxa>0,x∈(-∞,1],n≥2,
即a>-[(
)x+(
)x+…+(
)x],
∵y=-(
)x,k=1,2,3…n-1,在(-∞,1]上都是增函数,
∴y=-[(
)x+(
)x+…+(
)x],在(-∞,1]上也是增函数,
从而它在x=1时取得最大值-(
+
+…+
)=-
(n-1).
所以a>-[(
)x+(
)x+…+(
)x],成立.
n≥2
只需a>-
,
故a的取值范围是{a|a>-
}.
即a>-[(
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
∵y=-(
| k |
| n |
∴y=-[(
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
从而它在x=1时取得最大值-(
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| 1 |
| 2 |
所以a>-[(
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
n≥2
只需a>-
| 1 |
| 2 |
故a的取值范围是{a|a>-
| 1 |
| 2 |
点评:本题综合考查了函数的性质的运用,解决不等式恒成立问题时,注意根据单调性求解最值问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设P(x,2)为角α终边上的一点,且sinα=
,则tanα=( )
| ||
| x |
| A、1 | B、-1 | C、±1 | D、±2 |
观察下列各式:72=49,73=343,74=2410,75=16807 …则72015的末两位数为( )
| A、01 | B、07 | C、43 | D、49 |
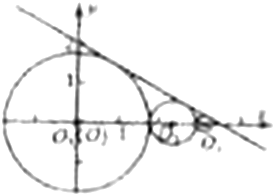 设O1,O2,…,On,…是坐标平面上圆心在x轴非负半轴上的一列圆(其中O1为坐标原点),且圆On和圆On+1相外切,并均与直线x+
设O1,O2,…,On,…是坐标平面上圆心在x轴非负半轴上的一列圆(其中O1为坐标原点),且圆On和圆On+1相外切,并均与直线x+