题目内容
已知函数f(x)是定义在实数集R上的不恒为零的偶函数,且对任意实数x都有xf(x+1)=(1+x)f(x),则f(
)的值是( )
| 2013 |
| 2 |
A、
| ||
| B、1 | ||
C、
| ||
| D、0 |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:由xf(x+1)=(1+x)f(x)结构来看,选用递推的方法,用赋值法依次求出f(
)=0,f(
)=0.f(
)=0,f(
)=0,于是可以找到规律,问题得以解决.
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
解答:
解:∵xf(x+1)=(1+x)f(x),
令x=-
,
则-
f(-
+1)=(1-
)f(-
),
∴f(
)=0,
同理可求 f(
)=0,f(
)=0,f(
)=0,
由以上可得f(
)=0,x∈2n+1.n∈N,
所以f(
)=0.
故选:D.
令x=-
| 1 |
| 2 |
则-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴f(
| 1 |
| 2 |
同理可求 f(
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
由以上可得f(
| x |
| 2 |
所以f(
| 2013 |
| 2 |
故选:D.
点评:本题主要考查抽象函数用递推的方法求函数值,这类问题关键是将条件和结论有机地结合起来,作适当变形,把握递推的规律.解题中要注意函数奇偶性的应用.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
设P是椭圆
+
=1上一点,F1,F2是椭圆的两个焦点,
•
=0,则△F1PF2面积是( )
| x2 |
| 25 |
| y2 |
| 5 |
| PF1 |
| PF2 |
| A、5 | B、10 | C、8 | D、9 |
以下命题:
(1)z-
是纯虚数
(2)z1+z2∈R?z1=
(3)z1-z2>0?z1>z2
(4)z∈R?z=
(5)z为纯虚数?z+
=0
其中正确命题的个数是( )
(1)z-
. |
| z |
(2)z1+z2∈R?z1=
. |
| z2 |
(3)z1-z2>0?z1>z2
(4)z∈R?z=
. |
| z |
(5)z为纯虚数?z+
. |
| z |
其中正确命题的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知等比数列{an}的前n项和为Sn,且满足
=5,则公比q=( )
| S4 |
| S2 |
A、±
| ||
B、
| ||
| C、±2 | ||
| D、2 |
已知f(x)是定义在R上的奇函数,且x≥0时f(x)的图象如图所示,则f(-2)=( )
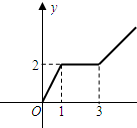
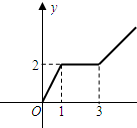
| A、-3 | B、-2 | C、-1 | D、2 |
已知某程序框图如图所示,则执行该程序后输出的结果是( )


| A、-1 | ||
B、
| ||
| C、2 | ||
| D、1 |
经过两直线l1:2x-3y+2=0与l2:3x-4y-2=0的交点,且平行于直线4x-2y+7=0的直线方程是( )
| A、x-2y+9=0 |
| B、4x-2y+9=0 |
| C、2x-y-18=0 |
| D、x+2y+18=0 |