题目内容
函数f′(x)是R上的可导函数,x≠0时,f′(x)+
>0,则函数g(x)=f(x)+
的零点个数为( )
| f(x) |
| x |
| 1 |
| x |
| A、3 | B、2 | C、1 | D、0 |
考点:利用导数研究函数的单调性,函数零点的判定定理
专题:
分析:①x>0时,由 xf'(x)+f(x)=(xf(x))'>0,得g(x)>
对任何大于零的x成立,所以显然在x轴正半轴不可能有零点;
②x<0时,由xf'(x)+f(x)<0,得g(x)=
<
,此时
总是负数,小于
是不可能与x轴有交点的.所以没有零点.
| 1 |
| x |
②x<0时,由xf'(x)+f(x)<0,得g(x)=
| xf(x)+1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
解答:
解:①x>0时,已知条件就是在说:xf'(x)+f(x)=(xf(x))'>0,
由于g(x)=
,且xf(x)>0f(0)=0,
∴g(x)>
对任何大于零的x成立,所以显然在x轴正半轴不可能有零点;
②x<0时,已知条件就是在说 xf'(x)+f(x)<0,
∴xf(x)>0f(0)=0 (x<0),
∴g(x)=
<
,
此时
总是负数,小于
是不可能与x轴有交点的.
所以没有零点,
故选:D.
由于g(x)=
| xf(x)+1 |
| x |
∴g(x)>
| 1 |
| x |
②x<0时,已知条件就是在说 xf'(x)+f(x)<0,
∴xf(x)>0f(0)=0 (x<0),
∴g(x)=
| xf(x)+1 |
| x |
| 1 |
| x |
此时
| 1 |
| x |
| 1 |
| x |
所以没有零点,
故选:D.
点评:本题考察了函数的单调性,函数的零点问题,导数的应用,是一道综合题.

练习册系列答案
相关题目
以下命题:
(1)z-
是纯虚数
(2)z1+z2∈R?z1=
(3)z1-z2>0?z1>z2
(4)z∈R?z=
(5)z为纯虚数?z+
=0
其中正确命题的个数是( )
(1)z-
. |
| z |
(2)z1+z2∈R?z1=
. |
| z2 |
(3)z1-z2>0?z1>z2
(4)z∈R?z=
. |
| z |
(5)z为纯虚数?z+
. |
| z |
其中正确命题的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知f(x)是定义在R上的奇函数,且x≥0时f(x)的图象如图所示,则f(-2)=( )
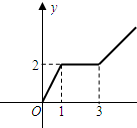
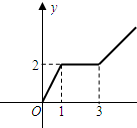
| A、-3 | B、-2 | C、-1 | D、2 |
按一定规律排列的数列2,5,11,23,47,x,…中的x应为( )
| A、97 | B、95 | C、93 | D、90 |
已知某程序框图如图所示,则执行该程序后输出的结果是( )


| A、-1 | ||
B、
| ||
| C、2 | ||
| D、1 |
如果直线a和直线b是异面直线,直线c∥a,那么直线b与c( )
| A、异面 | B、相交 |
| C、平行 | D、异面或相交 |
在等比数列{an}中,a1=1,且|q|≠1,若am=a2a3a4,则m=( )
| A、5 | B、6 | C、7 | D、8 |
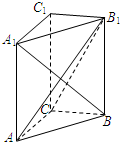 如图,在直三棱柱ABC-A1B1C1中,已知CA=CB=1,AA1=2,∠BCA=90°.
如图,在直三棱柱ABC-A1B1C1中,已知CA=CB=1,AA1=2,∠BCA=90°.