题目内容
已知三次函数f(x)=
x3-(4m-1)x2+(15m2-2m-7)x+2在x∈(-∞,+∞)是增函数,则m的取值范围是( )
| 1 |
| 3 |
| A、m<2或m>4 |
| B、2≤m≤4 |
| C、2<m<4 |
| D、-4<m<-2 |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:先求出f′(x)=x2-2(4m-1)x+(15m2-2m-7)>0,通过△=4(4m-1)2-4(15m2-2m-7)≤0,解出即可.
解答:
解:∵f(x)=
x3-(4m-1)x2+(15m2-2m-7)x+2,
∴f′(x)=x2-2(4m-1)x+(15m2-2m-7)>0,
∴△=4(4m-1)2-4(15m2-2m-7)≤0,
解得:2≤m≤4,
故选:B.
| 1 |
| 3 |
∴f′(x)=x2-2(4m-1)x+(15m2-2m-7)>0,
∴△=4(4m-1)2-4(15m2-2m-7)≤0,
解得:2≤m≤4,
故选:B.
点评:本题考察了函数的单调性,导数的应用,是一道基础题.

练习册系列答案
相关题目
以下命题:
(1)z-
是纯虚数
(2)z1+z2∈R?z1=
(3)z1-z2>0?z1>z2
(4)z∈R?z=
(5)z为纯虚数?z+
=0
其中正确命题的个数是( )
(1)z-
. |
| z |
(2)z1+z2∈R?z1=
. |
| z2 |
(3)z1-z2>0?z1>z2
(4)z∈R?z=
. |
| z |
(5)z为纯虚数?z+
. |
| z |
其中正确命题的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
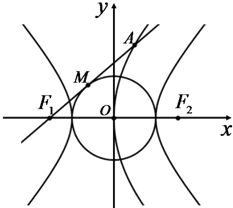 如图,双曲线C1:
如图,双曲线C1:| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知f(x)是定义在R上的奇函数,且x≥0时f(x)的图象如图所示,则f(-2)=( )
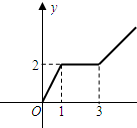
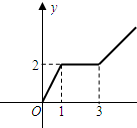
| A、-3 | B、-2 | C、-1 | D、2 |
按一定规律排列的数列2,5,11,23,47,x,…中的x应为( )
| A、97 | B、95 | C、93 | D、90 |
如果直线a和直线b是异面直线,直线c∥a,那么直线b与c( )
| A、异面 | B、相交 |
| C、平行 | D、异面或相交 |
两变量具有线性相关关系,且负相关,则相应的线性回归方程y=bx+a满足( )
| A、b=0 | B、b=1 |
| C、b<0 | D、b>0 |
