题目内容
在△ABC中,a=2,b=
,c=30°,则△ABC的面积是( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:正弦定理
专题:解三角形
分析:由a,b,sinC的值,利用三角形面积公式即可求出三角形ABC面积.
解答:
解:∵在△ABC中,a=2,b=
,c=30°,
∴S△ABC=
absinC=
×2×
×
=
.
故选:B.
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
故选:B.
点评:此题考查了三角形的面积公式,熟练掌握三角形面积公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知f(x)是定义在R上的奇函数,且x≥0时f(x)的图象如图所示,则f(-2)=( )
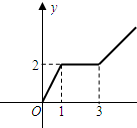
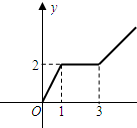
| A、-3 | B、-2 | C、-1 | D、2 |
已知某程序框图如图所示,则执行该程序后输出的结果是( )


| A、-1 | ||
B、
| ||
| C、2 | ||
| D、1 |
如果直线a和直线b是异面直线,直线c∥a,那么直线b与c( )
| A、异面 | B、相交 |
| C、平行 | D、异面或相交 |
关于x的不等式x2-2ax-8a2<0的解集为(x1,x2),且x12-x22=15,则实数a=( )
A、
| ||||||||
B、-
| ||||||||
C、-
| ||||||||
D、-
|
在等比数列{an}中,a1=1,且|q|≠1,若am=a2a3a4,则m=( )
| A、5 | B、6 | C、7 | D、8 |
经过两直线l1:2x-3y+2=0与l2:3x-4y-2=0的交点,且平行于直线4x-2y+7=0的直线方程是( )
| A、x-2y+9=0 |
| B、4x-2y+9=0 |
| C、2x-y-18=0 |
| D、x+2y+18=0 |