题目内容
已知函数y=f(x)对任意的实数x都有
=
+1,且f(1)=1,则f(2013)=( )
| 1 |
| f(x+2) |
| 1 |
| f(x+1) |
A、
| ||
B、
| ||
| C、2013 | ||
| D、2014 |
考点:抽象函数及其应用,函数的值
专题:函数的性质及应用
分析:利用赋值法,分别求出f(1)…f(5)得出f(x)=
,故求出答案.
| 1 |
| x |
解答:
解;∵
=
+1,
∴f(x+1)f(x+2)=f(x+1)-f(x+2),
令x=0,
则f(0+1)f(0+2)=f(0+1)-f(0+2),
∴f(2)=
,
再令x=1,则f(3)=
,
同理求得f(4)=
,f(5)=
,
于是可得f(x)=
,
故f(2013)=
.
故选:B.
| 1 |
| f(x+2) |
| 1 |
| f(x+1) |
∴f(x+1)f(x+2)=f(x+1)-f(x+2),
令x=0,
则f(0+1)f(0+2)=f(0+1)-f(0+2),
∴f(2)=
| 1 |
| 2 |
再令x=1,则f(3)=
| 1 |
| 3 |
同理求得f(4)=
| 1 |
| 4 |
| 1 |
| 5 |
于是可得f(x)=
| 1 |
| x |
故f(2013)=
| 1 |
| 2013 |
故选:B.
点评:本题主要考查了抽象函数及其应用,考查分析问题和解决问题的能力,属于中档题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设P是椭圆
+
=1上一点,F1,F2是椭圆的两个焦点,
•
=0,则△F1PF2面积是( )
| x2 |
| 25 |
| y2 |
| 5 |
| PF1 |
| PF2 |
| A、5 | B、10 | C、8 | D、9 |
以下命题:
(1)z-
是纯虚数
(2)z1+z2∈R?z1=
(3)z1-z2>0?z1>z2
(4)z∈R?z=
(5)z为纯虚数?z+
=0
其中正确命题的个数是( )
(1)z-
. |
| z |
(2)z1+z2∈R?z1=
. |
| z2 |
(3)z1-z2>0?z1>z2
(4)z∈R?z=
. |
| z |
(5)z为纯虚数?z+
. |
| z |
其中正确命题的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知f(x)是定义在R上的奇函数,且x≥0时f(x)的图象如图所示,则f(-2)=( )
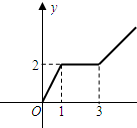
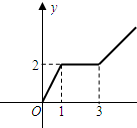
| A、-3 | B、-2 | C、-1 | D、2 |
在等比数列{an}中,a1=1,且|q|≠1,若am=a2a3a4,则m=( )
| A、5 | B、6 | C、7 | D、8 |
