题目内容
若函数f(x)=x3-3bx+b在(0,1)内有极小值,则( )
| A、b>0 | ||
| B、b<1 | ||
| C、0<b<1 | ||
D、b<
|
考点:利用导数研究函数的极值
专题:计算题,导数的综合应用
分析:首先求出函数的导数,然后令导数为零,求出函数的极小值点,最后确定b的范围.
解答:
解:由题意得b>0,
又f′(x)=3x2-3b,
令f′(x)=0,则x=±
,
由于x=
处附近导数左负右正,则为极小值点,
又函数f(x)=x3-3bx+b在区间(0,1)内有极小值,
∴0<
<1,
∴b∈(0,1),
故选C.
又f′(x)=3x2-3b,
令f′(x)=0,则x=±
| b |
由于x=
| b |
又函数f(x)=x3-3bx+b在区间(0,1)内有极小值,
∴0<
| b |
∴b∈(0,1),
故选C.
点评:本题考查运用函数的导数求解函数的极值问题,同时考查了运算的能力,属于中档题.

练习册系列答案
相关题目
若定义在R上的函数f(x)的导函数为f'(x),且满足f'(x)>f(x),则f(2011)与f(2009)e2的大小关系为( )
| A、f(2011)<f(2009)e2 |
| B、f(2011)=f(2009)e2 |
| C、f(2011)>f(2009)e2 |
| D、不能确定 |
集合A={x|y=
},B={y|y=x2-1},则∁RA∪B=( )
| x2-4 |
| A、(-2,+∞) |
| B、[-2,+∞) |
| C、(-1,+∞) |
| D、[-1,+∞) |
若变量x、y满足
,若2x-y的最大值为-1,则a=( )
|
| A、-1 | B、1 | C、-2 | D、2 |
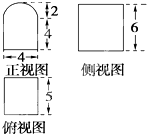
某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )

| A、92+24π |
| B、82+14π |
| C、92+14π |
| D、82+24π |
已知M={x|x2-3x<0},N={x|y=
},则M∩(∁RN)=( )
| x-2 |
| A、(0,1) |
| B、(0,2) |
| C、(0,3) |
| D、(-∞,2) |
