题目内容

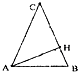如图，在△ABC中，cos
C
2
=
2
5
5
，
AH
•
BC
=0，
AB
•（
CA
+
CB
）=0，则过点C，以A、H为两焦点的双曲线的离心率为
 
．
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由已知中在△ABC中，cos
C
2
=
2
5
5
，
AH
•
BC
=0，
AB
•（
CA
+
CB
）=0，H在BC边上，我们根据向量垂直的数量积为0，及二倍角的正切公式，易得△ABC是一个顶角正切为
4
3
的等腰三角形，AH为腰上高，由此设出各边的长度，然后根据双曲线的性质及双曲线离心率的定义，即可求出答案．
解答： 解：由已知中
AH
•
BC
=0可得：AH为BC边上的高
又由
AB
•（
CA
+
CB
）=0可得：CA=CB
又由cos
C
2
=
2
5
5
，可得tanC=
4
3

令AH=4x，则CH=3x，AC=BC=5x，BH=2x，
则过点C，以A、H为两焦点的双曲线中，2a=5x-3x=2x，2c=4x
则过点C，以A、H为两焦点的双曲线的离心率e=2．
故答案为：2
点评：本题考查的知识点是双曲线的简单性质，其中根据已知求出满足条件的△ABC的形状进而求出各边长是解答本题的关键．
练习册系列答案
相关题目
已知等差数列{an}中，满足a3=5且a1，a2，a4成等比数列．
（Ⅰ）求an；
（Ⅱ）若数列{an}的公差为非零的常数，且bn=
25
an•an+1
，记数列{bn}的前n项和为Tn，当Tn≤λ恒成立，求λ的最小值．
若f（x）是以2为周期的函数，且f（2）=2，则f（4）=
 
．
f（x）是定义在R上的偶函数，当x＜0时，f（x）+x•f′（x）＜0，且f（-4）=0，则不等式xf（x）＞0的解集为
 
．
定义函数f（x）=[x•[x]]，其中[x]表示不超过x的最大整数，如[1.3]=1，[-2.5]=-3，当x∈[0，n）（n∈N*）时，设函数f（x）的值域为集合A，设A中元素个数为an，则使
an+49
n
取最小值时，n的值为
 
．
如图，在高出地面30m的小山顶C上建造一座电视塔，今在距离B点60m的地面上取一点A，在此点测得CD所张的角为45°（即∠CAD=45°），则电视塔CD的高度是
 
．
设M和m分别表示函数y=
1
3
cosx-1的最大值和最小值，则M+m等于
 
．
已知f（
2
x
+1）=lgx，则f（21）=
 
．
利用不等式求最值，下列运用错误的是（　　）
A、若x＜-1，则2x-1+
1
2x-1
≤-2
B、
x2+2
x2+1
≥2
C、y=2x+
1
2x
≥2
D、已知ab＞0，
b
a
+
a
b
≥2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网