题目内容
 如图所示,在三棱锥P-ABC中,E、F分别为AC、BC的中点.
如图所示,在三棱锥P-ABC中,E、F分别为AC、BC的中点.(1)证明:EF∥平面PAB;(2)若PA=PB,CA=CB,求证:AB⊥PC;
(3)若PB=AB=CB,ABC=120°,PB⊥面ABC,求二面角P-AC-B的正切值.
考点:二面角的平面角及求法,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)依题意知E,F为中位线推断出EF∥AB,依据线面平行的判定定理推断出EF∥平面PAB.
(2)取AB的中点G,连结PG,CG,根据PA=PB,CA=CB,判断出△PAB,△ACB均为等腰三角形进而可推断出AB⊥PG,AB⊥CG,利用线面垂直的判定定理得出AB⊥平面GPC,最后根据线面垂直的性质得出AB⊥PC的结论.
(2)取AB的中点G,连结PG,CG,根据PA=PB,CA=CB,判断出△PAB,△ACB均为等腰三角形进而可推断出AB⊥PG,AB⊥CG,利用线面垂直的判定定理得出AB⊥平面GPC,最后根据线面垂直的性质得出AB⊥PC的结论.
解答:
证明:(1)∵E,F为AC、BC的中点,
∴EF∥AB,
∵AB?平面PAB,EF?平面PAB,
∴EF∥平面PAB.
(2)取AB的中点G,连结PG,CG,
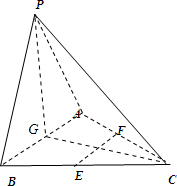
∵PA=PB,CA=CB,
∴AB⊥PG,AB⊥CG,
∵PG?平面GPC,CG?平面GPC,且PG∩CG=C,
∴AB⊥平面GPC,
∵PC?平面GPC,
∴AB⊥PC.
解:(3)连接BF,PF,
∵BA=CB,
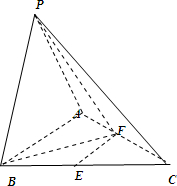
∴BF⊥AC,
又∵PB⊥面ABC,AC?面ABC,
∴PB⊥AC,
又∵PB∩BF=B,PB,BF?平面PBF,
∴∠PFB即为二面角P-AC-B的平面角,
设PB=AB=CB=a,ABC=120°,
∴BF=
a,
∴tan∠PFB=
=2,
即二面角P-AC-B的正切值为2.
∴EF∥AB,
∵AB?平面PAB,EF?平面PAB,
∴EF∥平面PAB.
(2)取AB的中点G,连结PG,CG,

∵PA=PB,CA=CB,
∴AB⊥PG,AB⊥CG,
∵PG?平面GPC,CG?平面GPC,且PG∩CG=C,
∴AB⊥平面GPC,
∵PC?平面GPC,
∴AB⊥PC.
解:(3)连接BF,PF,
∵BA=CB,

∴BF⊥AC,
又∵PB⊥面ABC,AC?面ABC,
∴PB⊥AC,
又∵PB∩BF=B,PB,BF?平面PBF,
∴∠PFB即为二面角P-AC-B的平面角,
设PB=AB=CB=a,ABC=120°,
∴BF=
| 1 |
| 2 |
∴tan∠PFB=
| PB |
| BF |
即二面角P-AC-B的正切值为2.
点评:本题主要考查了直线和平面平行的判定和直线与平面垂直的判定.综合考查了学生对基础知识的运用.

练习册系列答案
相关题目
设集合A={-1,0,1},B={x∈R|x>0},则A∩B=( )
| A、{-1,0} | B、{-1} |
| C、{0,1} | D、{1} |
某几何体的三视图如图所示,则它的体积为( )
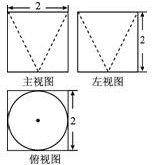

A、8-
| ||
B、8-
| ||
| C、8-2π | ||
D、
|

 如图是自治区环境监测网从8月21日至25日五天监测到甲城市和乙城市的空气质量指数数据,用茎叶图表示:
如图是自治区环境监测网从8月21日至25日五天监测到甲城市和乙城市的空气质量指数数据,用茎叶图表示: