题目内容
对任意实数组x1,x2,…,xn,记它们中最小的数为f(x1,x2,…,xn),给出下述结论:
①函数y=f(4x,2-3x)的图象为一条直线;
②函数y=f(x,2-x)的最大值等于1;
③函数y=f(x2+2x,x2-2x)一定为偶函数;
④对a>0,b>0,f(a,b,
)的最大值为
.
其中,正确命题的序号有 .
①函数y=f(4x,2-3x)的图象为一条直线;
②函数y=f(x,2-x)的最大值等于1;
③函数y=f(x2+2x,x2-2x)一定为偶函数;
④对a>0,b>0,f(a,b,
| 1 |
| a2+b2 |
| 3 |
| ||
其中,正确命题的序号有
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:①根据最小数求出函数式,即可判断图象;②求出函数式,即可得到最大值;③求出函数式,用分段表示,合并成f(x)=x2-2|x|,即可判断奇偶性;④由最小数的定义得到故f(a,b,
)≤
,再由基本不等式即可得到最大值,注意等号成立的条件.
| 1 |
| a2+b2 |
| 3 | ab•
| ||
解答:
解:①f(4x,2-3x)=
,的图象为折线,故①是错误的;
②f(x,2-x)=
的最大值为1,故②正确;
③函数y=f(x2+2x,x2-2x)=
,故函数f(x)=x2-2|x|,f(-x)=f(x),即f(x)是偶函数,故③正确;
对④,由于f(a,b,
)≤a,f(a,b,
)≤b,f(a,b,
)≤
,
故f(a,b,
)≤
≤
=
,
当且仅当a=b=
,即a=b=
时取等号,故④也正确.
故答案为:②③④.
|
②f(x,2-x)=
|
③函数y=f(x2+2x,x2-2x)=
|
对④,由于f(a,b,
| 1 |
| a2+b2 |
| 1 |
| a2+b2 |
| 1 |
| a2+b2 |
| 1 |
| a2+b2 |
故f(a,b,
| 1 |
| a2+b2 |
| 3 | ab•
| ||
| 3 | ab•
| ||||
| 3 |
| ||
当且仅当a=b=
| 1 |
| a2+b2 |
| 3 |
| ||
故答案为:②③④.
点评:本题主要考查分段函数的解析式的求法,以及图象和性质,考查函数的最值和奇偶性,以及基本不等式的运用,注意等号成立的条件.

练习册系列答案
相关题目
cos47°cos17°+cos43°cos73°的值为( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
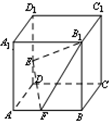 (理科)已知如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1,AB上的点(不含顶点).则下列说法正确的是
(理科)已知如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1,AB上的点(不含顶点).则下列说法正确的是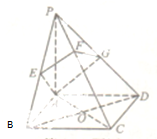 如图,四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,过A点的截面AEFG分别交PB,PC,PD于点E,F,G,且PB⊥AE,PD⊥AG.下列结论正确的是
如图,四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,过A点的截面AEFG分别交PB,PC,PD于点E,F,G,且PB⊥AE,PD⊥AG.下列结论正确的是