题目内容
已知平面向量
,
满足|
|=|
|=1,且
与
-
的夹角为120°,则|(1-t)
+2t
|(t∈R)的取值范围是 .
| α |
| β |
| α |
| β |
| α |
| β |
| α |
| α |
| β |
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:根据|
|=|
|=1,且
与
-
的夹角为120°,算出
•(
-
)=-
|
-
|,又|
-
|2=2-2
•
,可解得
•
=1,|(1-t)
+2t
|2=(1-t)2
2+4t(1-t)
•
+4t2
2=3t2+1≥1.即可得出结论.
| α |
| β |
| α |
| β |
| α |
| α |
| β |
| α |
| 1 |
| 2 |
| β |
| α |
| β |
| α |
| α |
| β |
| α |
| β |
| α |
| β |
| α |
| α |
| β |
| β |
解答:
解:∵|
|=|
|=1,且
与
-
的夹角为120°,
∴
•(
-
)=-
|
-
|,
•
=-
|
-
|+1,①
又|
-
|2=2-2
•
,②
∴由①②联立可得
•
=1,
∴|(1-t)
+2t
|2=(1-t)2
2+4t(1-t)
•
+4t2
2=3t2+1≥1.
∴|(1-t)
+2t
|的取值范围为[1,+∞).
故答案为:[1,+∞).
| α |
| β |
| α |
| β |
| α |
∴
| α |
| β |
| α |
| 1 |
| 2 |
| β |
| α |
| α |
| β |
| 1 |
| 2 |
| β |
| α |
又|
| β |
| α |
| α |
| β |
∴由①②联立可得
| α |
| β |
∴|(1-t)
| α |
| β |
| α |
| α |
| β |
| β |
∴|(1-t)
| α |
| β |
故答案为:[1,+∞).
点评:本题着重考查了平面向量数量积的公式、向量模的公式和实数的平方为非负数的性质等知识,属于中档题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 图①是一个边长为(m+n)的正方形,小明将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )
图①是一个边长为(m+n)的正方形,小明将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )| A、(m+n)2-(m-n)2=4mn |
| B、(m+n)2-(m2+n2)=2mn |
| C、(m-n)2+2mn=m2+n2 |
| D、(m+n)(m-n)=m2-n2 |
设集合S={y|y=(
)x-1,x∈R},T={y|y=log2(x+2)},S∪T=( )
| 1 |
| 2 |
| A、S | B、T |
| C、R | D、[-1,+∞) |
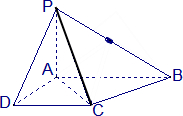 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=