Question

已知E为不等式组

x+y≥2 x+2y≤4 y≥1

，表示区域内的一点，过点E的直线l与圆M：（x-1）²+y²=9相交于A，C两点，过点E与l垂直的直线交圆M于B、D两点，当AC取最小值时，四边形ABCD的面积为（　　）

• A、12
• B、6

  7

• C、12

  2

• D、4

  5

Answer 1

考点：简单线性规划的应用

专题：不等式的解法及应用

分析：由约束条件作出可行域，由圆的方程画出圆，可知可行域内距离圆心最远的点为满足条件的E点，求出E与M的距离，解直角三角形求得AC的长度，则四边形ABCD的面积为AC长度与BD长度乘积的一半．

解答： 解：由约束条件

x+y≥2 x+2y≤4 y≥1

作可行域如图，

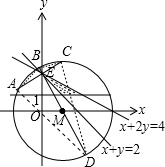
圆M：（x-1）²+y²=9的圆心为M（1，0），半径为3．
E为图中阴影三角形及其内部一动点，
由图可知，当E点位于直线x+y=2与y轴交点时，E为可行域内距离圆心M最远的点．
此时当AC过E且与ME垂直时最短．与AC垂直的直线交圆得到直径BD．
|ME|=

5

，|AC|=2

32- 5 2

=4，
S_{四边形ABCD}=

1

2

×6×4=12．
故选：A

点评：本题考查简单的线性规划，考查数形结合的解题思想方法，关键是确定使AC最短时的E的位置，是中档题．