题目内容
椭圆
+
=1的焦点坐标为（ ）
| x2 |
| 4 |
| y2 |
| 3 |
| A、（±1，0） | ||
B、（±
| ||
| C、（±2，0） | ||
| D、（0，±1） |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：确定椭圆中a，b，c，可得椭圆
+
=1的焦点坐标．
| x2 |
| 4 |
| y2 |
| 3 |
解答：
解：椭圆
+
=1中a=2，b=
，∴c=1，
∴椭圆
+
=1的焦点坐标为（±1，0）．
故选：A．
| x2 |
| 4 |
| y2 |
| 3 |
| 3 |
∴椭圆
| x2 |
| 4 |
| y2 |
| 3 |
故选：A．
点评：本题考查椭圆的简单性质，确定a，b，c是关键，属于基础题．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
已知随机变量X服从正态分布N（3，σ2），且P（X＜2）=0.3，则P（2＜X＜4）的值等于（ ）
| A、0.5 | B、0.2 |
| C、0.3 | D、0.4 |
设ξ的分布列为P（ξ=k）=C
（
）k（
）5-k，（k=0，1，2，3，4，5），求D（3ξ）=（ ）
k 5 |
| 1 |
| 3 |
| 2 |
| 3 |
| A、10 | B、30 | C、15 | D、5 |
由直线x=-
，x=-2，曲线y=
及x轴所围图形的面积是（ ）
| 1 |
| 2 |
| 1 |
| x |
A、
| ||
B、
| ||
C、
| ||
| D、2ln2 |
已知函数f（x+1）是偶函数，且x＞1时，f′（x）＜0恒成立，又f（4）=0，则（x+3）f（x+4）＜0的解集为（ ）
| A、（-∞，-2）∪（4，+∞） |
| B、（-6，-3）∪（0，4） |
| C、（-∞，-6）∪（4，+∞） |
| D、（-6，-3）∪（0，+∞） |
设?的分布列为
又设y=2?+5 则 Ey=（ ）
| ? | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f（x）=ax3+bx2+cx+d的图象如图所示，则一定有（ ）
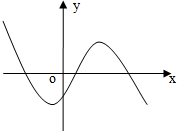
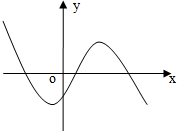
| A、a＜0 b＞0 c＞0 d＜0 |
| B、a＜0 b＜0 c＞0 d＜0 |
| C、a＜0 b＞0 c＜0 d＜0 |
| D、a＜0 b＜0 c＜0 d＜0 |
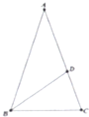学习“三角”时，小明同学在参考书上看到求sin18°精确值的一种方法，具体如下：设等腰△ABC的顶角∠A=36°．底角∠B的平分线交腰AC于D，且BC=1（如图），则AD=BD=1，于是，在△BCD中，可得CD=2sin18°．由△BAC∽△CBD得| AC |
| BC |
| BD |
| CD |
| 1+2sin18° |
| 1 |
| 1 |
| 2sin18° |
| ||
| 4 |
| π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
| A、关于x的方程α•4x+β•2x+α=0有实数解 | ||
| B、关于x的方程α•（log4x）2+β•log4x-α=0无实数解 | ||
C、关于x的方程sinx=
| ||
D、关于x的方程cosx=
|