题目内容
已知函数f(x+1)是偶函数,且x>1时,f′(x)<0恒成立,又f(4)=0,则(x+3)f(x+4)<0的解集为( )
| A、(-∞,-2)∪(4,+∞) |
| B、(-6,-3)∪(0,4) |
| C、(-∞,-6)∪(4,+∞) |
| D、(-6,-3)∪(0,+∞) |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:由函数f(x+1)是偶函数知,f(x)图象关于x=1对称,又x>1时,f′(x)<0恒成立,知道f(x)在(1,+∞)递减,在(-∞,1)上递增,再结合f(4)=0,可得到(x-1)f(x)<0的解集,运用换元法可求得(x+3)f(x+4)<0的解.
解答:
解:∵函数f(x+1)是偶函数,∴其图象关于y轴对称,
∵f(x)的图象是由f(x+1)的图象向右平移1个单位得到的,
∴f(x)的图象关于x=1对称,
又∵x>1时,f′(x)<0恒成立,所以f(x)在(1,+∞)上递减,在(-∞,1)上递增,
又f(4)=0,∴f(-2)=0,
∴当x∈(-∞,-2)∪(4,+∞)时,f(x)<0;当x∈(-2,1)∪(1,4)时,f(x)>0;
∴对于(x-1)f(x)<0,当x∈(-2,1)∪(4,+∞)时成立,
∵(x+3)f(x+4)<0可化为(x+4-1)f(x+4)<0,
∴由-2<x+4<1或x+4>4得所求的解为-6<x<-3或x>0.
故选D
∵f(x)的图象是由f(x+1)的图象向右平移1个单位得到的,
∴f(x)的图象关于x=1对称,
又∵x>1时,f′(x)<0恒成立,所以f(x)在(1,+∞)上递减,在(-∞,1)上递增,
又f(4)=0,∴f(-2)=0,
∴当x∈(-∞,-2)∪(4,+∞)时,f(x)<0;当x∈(-2,1)∪(1,4)时,f(x)>0;
∴对于(x-1)f(x)<0,当x∈(-2,1)∪(4,+∞)时成立,
∵(x+3)f(x+4)<0可化为(x+4-1)f(x+4)<0,
∴由-2<x+4<1或x+4>4得所求的解为-6<x<-3或x>0.
故选D
点评:抽象函数问题一般借助于数形结合的思想解决,解题中要注意图象变换方法的运用.

练习册系列答案
相关题目
对于事件A和事件B,通过计算得到K2的观测值k≈4.526,下列说法正确的是( )
| A、在犯错误的概率不超过0.01的前提下认为事件A和事件B有关 |
| B、在犯错误的概率不超过0.05的前提下认为事件A和事件B有关 |
| C、在犯错误的概率不超过0.01的前提下认为事件A和事件B无关 |
| D、在犯错误的概率不超过0.05的前提下认为事件A和事件B无关 |
已知x,y为实数,若3x+5y>3-y+5-x,则( )
| A、x+y>0 |
| B、x+y<0 |
| C、x-y<0 |
| D、x-y>0 |
若a?α,b?α,a∥α,条件甲是“a∥b”,条件乙是“b∥α”,则条件甲是条件乙的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
椭圆
+
=1的焦点坐标为( )
| x2 |
| 4 |
| y2 |
| 3 |
| A、(±1,0) | ||
B、(±
| ||
| C、(±2,0) | ||
| D、(0,±1) |
动点P满足
=
+λ[
+
],λ>0,则动点P的轨迹一定通过△ABC的( )
| OP |
| OA |
| ||
|
|
| ||
|
|
| A、重心 | B、垂心 | C、内心 | D、外心 |
运行以下程序:

得到的结果是( )

得到的结果是( )
| A、j-1 | B、j | C、10 | D、9 |
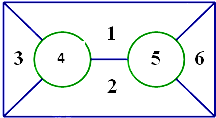 有六种不同颜色,给如图的六个区域涂色,要求相邻区域不同色,不同的涂色方法共有( )
有六种不同颜色,给如图的六个区域涂色,要求相邻区域不同色,不同的涂色方法共有( )| A、4320 | B、2880 |
| C、1440 | D、720 |
如果执行下面的算法语句后输出结果是8,则输入的值是( )


| A、3 | B、5或12- |
| C、12 | D、4或12 |