题目内容
10.如果直线l将圆x2+y2+2x-4y=0平分,且不过第一象限,那么l的斜率的取值范围是( )| A. | [0,2] | B. | (0,2) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,-2] |
分析 将圆的方程化为标准方程,找出圆心C坐标,由于kOC=-2,根据直线l将圆x2+y2+2x-4y=0平分得到直线l过圆心C(-1,2),且不过第一象限,即可求出k的范围.
解答 解:将圆的方程化为标准方程得:(x+1)2+(y-2)2=5,
∴圆心C(-1,2),
由于kOC=-2,根据直线l将圆x2+y2+2x-4y=0平分得到直线l过圆心C(-1,2),且不过第一象限,
∴直线l斜率k的范围为(-∞,-2].
故选D.
点评 此题考查了直线与圆相交的性质,利用了数形结合的思想,熟练掌握数形结合思想是解本题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
18.已知函数$f(x)=\left\{\begin{array}{l}{2^x}-1({x≤0})\\ f({x-1})+1({x>0})\end{array}\right.$,把函数g(x)=f(x)-x的零点的顺序排列成一个数列,则该数列的通项公式为( )
| A. | ${a_n}=\frac{{n({n-1})}}{2}$ | B. | an=n(n-1) | C. | an=n-1 | D. | ${a_n}={2^n}-2$ |
2.若等差数列{an}的前n项和为Sn,且S5=20,则a3等于( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
8.已知命题p:$\frac{1}{a}$>$\frac{1}{4}$,命题q:?x∈R,ax2+1>0,则p成立是q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图是一个求函数值的算法流程图,若输入的x的值为5,则输出的y的值为-15.
如图是一个求函数值的算法流程图,若输入的x的值为5,则输出的y的值为-15.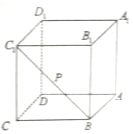 如图,点P是正方体ABCD-A1B1C1D1的面对角线BC1(线段BC1)上运动,给出下列五个命题:
如图,点P是正方体ABCD-A1B1C1D1的面对角线BC1(线段BC1)上运动,给出下列五个命题: