题目内容
9.已知f(x)是奇函数,当x>0时,f(x)=2x-a-1,若f(-1)=$\frac{3}{4}$,则a等于( )| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
分析 由题意和奇函数的性质得f(1)=-$\frac{3}{4}$,代入解析式由指数的运算性质求出a的值.
解答 解:∵f(x)是奇函数,f(-1)=$\frac{3}{4}$,
∴f(1)=-$\frac{3}{4}$,
∵当x>0时,f(x)=2x-a-1,
∴f(1)=21-a-1=$-\frac{3}{4}$,则21-a=$\frac{1}{4}$=2-2,
即1-a=-2,解得a=3,
故选:C.
点评 本题考查待定系数法求出指数函数的解析式,指数的运算性质,以及奇函数的性质,属于基础题.

练习册系列答案
相关题目
10.如果直线l将圆x2+y2+2x-4y=0平分,且不过第一象限,那么l的斜率的取值范围是( )
| A. | [0,2] | B. | (0,2) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,-2] |
19.直线x-y=0被圆x2+y2=1截得的弦长为( )
| A. | $\sqrt{2}$ | B. | 1 | C. | 4 | D. | 2 |
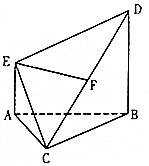 如图,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2,F为CD中点.
如图,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2,F为CD中点.
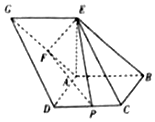 如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE
如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE