题目内容
8．已知命题p：$\frac{1}{a}$＞$\frac{1}{4}$，命题q：?x∈R，ax2+1＞0，则p成立是q成立的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 命题p：$\frac{1}{a}$＞$\frac{1}{4}$，解得0＜a＜4．命题q：?x∈R，ax2+1＞0，则a=0，或$\left\{\begin{array}{l}{a＞0}\\{△=0-4a＜0}\end{array}\right.$，解得a，即可判断出结论．
解答 解：命题p：$\frac{1}{a}$＞$\frac{1}{4}$，解得0＜a＜4．
命题q：?x∈R，ax2+1＞0，则a=0，或$\left\{\begin{array}{l}{a＞0}\\{△=0-4a＜0}\end{array}\right.$，解得a≥0．
则p成立是q成立的充分不必要条件．
故选：A．
点评 本题考查了不等式的解法与性质、二次函数的性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
9．若直线（a-1）x-2y+1=0与直线x-ay+1=0平行，则a=（ ）
| A． | -1或2 | B． | -1 | C． | 2 | D． | $\frac{1}{3}$ |
10．如果直线l将圆x2+y2+2x-4y=0平分，且不过第一象限，那么l的斜率的取值范围是（ ）
| A． | [0，2] | B． | （0，2） | C． | （-∞，0）∪（2，+∞） | D． | （-∞，-2] |
7．已知△ABC满足∠BAC=60°，BC=2，对于△ABC外接圆上一点D，满足∠BCD=45°，则BD=（ ）
| A． | $\sqrt{6}$ | B． | $\sqrt{3}$ | C． | $\frac{2\sqrt{3}}{3}$ | D． | $\frac{2\sqrt{6}}{3}$ |
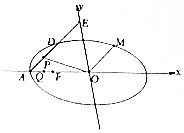已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{12}$=1（a＞2$\sqrt{3}$）的左焦点为F，左顶点为A，$\frac{1}{|OF|}$+$\frac{1}{|OA|}$=$\frac{3e}{|FA|}$，其中O为原点，e为椭圆的离心率，过点A作斜率为k（k≠0）的直线l交椭圆C于点D，交y轴于点E．
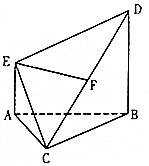如图，AE⊥平面ABC，AE∥BD，AB=BC=CA=BD=2AE=2，F为CD中点．