题目内容

2．若等差数列{an}的前n项和为Sn，且S5=20，则a3等于（　　）
A．3B．4C．5D．6

分析 利用等差数列的通项公式求和公式及其性质即可得出．

解答 解：由等差数列的求和公式及其性质可得：S5=$\frac{5（{a}_{1}+{a}_{5}）}{2}$=5a3=20，解得a3=4．
故选：B．

点评 本题考查了等差数列的通项公式求和公式及其性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
12．在空间直角坐标系Oxyz中，z轴上的点M到点A（1，0，2）与点B（1，-3，1）的距离相等，则点M的坐标是（　　）
A．（0，0，-3）B．（0，0，3）C．（0，0，$\sqrt{10}$）D．（0，0，-$\sqrt{10}$）
13．已知向量$\overrightarrow{a}$=（1，m），$\overrightarrow{b}$=（2，1）．若m实数，且（$\overrightarrow{a}$+$\overrightarrow{b}$）⊥$\overrightarrow{b}$，则m=（　　）
A．-7B．-6C．7D．6
10．如果直线l将圆x2+y2+2x-4y=0平分，且不过第一象限，那么l的斜率的取值范围是（　　）
A．[0，2]B．（0，2）C．（-∞，0）∪（2，+∞）D．（-∞，-2]
17．设△ABC的内角A，B，C所对的边长分别为a，b，c，若bcosC+ccosB=2acosA，则A=（　　）
A．$\frac{π}{6}$B．$\frac{π}{3}$C．$\frac{π}{4}$D．$\frac{π}{3}$或$\frac{2π}{3}$
7．已知△ABC满足∠BAC=60°，BC=2，对于△ABC外接圆上一点D，满足∠BCD=45°，则BD=（　　）
A．$\sqrt{6}$B．$\sqrt{3}$C．$\frac{2\sqrt{3}}{3}$D．$\frac{2\sqrt{6}}{3}$
3．已知集合A={x|x2-2x+2a-a2≤0}，B={x|sin（πx-$\frac{π}{3}}$）+$\sqrt{3}$cos（πx-$\frac{π}{3}}$）=0}．
（1）若2∈A，求a的取值范围；
（2）若A∩B恰有3个元素，求a的取值范围．
20．已知点P（x，y）在椭圆x2+4y2=4上，则$\frac{3}{4}{x^2}+2x-{y^2}$的最大值为（　　）
A．8B．7C．2D．-1
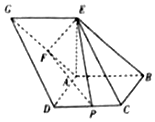1．如图，已知四边形ABCD和ABEG均为平行四边形，点E在平面ABCD内的射影恰好为点A，以BD为直径的圆经过点A，C，AG的中点为F，CD的中点为P，且AD=AB=AE
（Ⅰ）求证：平面EFP⊥平面BCE
（Ⅱ）求二面角P-EF-B的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网