题目内容
18.已知函数$f(x)=\left\{\begin{array}{l}{2^x}-1({x≤0})\\ f({x-1})+1({x>0})\end{array}\right.$,把函数g(x)=f(x)-x的零点的顺序排列成一个数列,则该数列的通项公式为( )| A. | ${a_n}=\frac{{n({n-1})}}{2}$ | B. | an=n(n-1) | C. | an=n-1 | D. | ${a_n}={2^n}-2$ |
分析 根据函数的零点的定义,构造两函数图象的交点,交点的横坐标即为函数的零点,再通过数列及通项公式的概念得所求的解.
解答 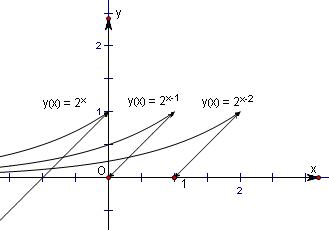 解:当x∈(-∞,0]时,
解:当x∈(-∞,0]时,
由g(x)=f(x)-x=2x-1-x=0,得2x=x+1.
令y=2x,y=x+1.
在同一个坐标系内作出两函数在区间
(-∞,0]上的图象,
由图象易知交点为(0,1),
故得到函数的零点为x=0.
当x∈(0,1]时,x-1∈(-1,0],
f(x)=f(x-1)+1=2x-1-1+1=2x-1,
由g(x)=f(x)-x=2x-1-x=0,得2x-1=x.
令y=2x-1,y=x.
在同一个坐标系内作出两函数在区间(0,1]上的图象,由图象易知交点为(1,1),
故得到函数的零点为x=1.
当x∈(1,2]时,x-1∈(0,1],f(x)=f(x-1)+1=2x-1-1+1=2x-2+1,
由g(x)=f(x)-x=2x-2+1-x=0,得2x-2=x-1.令y=2x-2,y=x-1.
在同一个坐标系内作出两函数在区间(1,2]上的图象,
由图象易知交点为(2,1),故得到函数的零点为x=2.
依此类推,当x∈(2,3],x∈(3,4],…,x∈(n,n+1]时,
构造的两函数图象的交点依次为(3,1),(4,1),…,(n+1,1),
得对应的零点分别为x=3,x=4,…,x=n+1.
故所有的零点从小到大依次排列为0,1,2,…,n+1.其对应的数列的通项公式为an=n-1.
故选:C.
点评 本题主要考查了函数零点的概念及零点的求法、数列的概念及简单表示;培养学生观察、分析、归纳、推理的能力;解题中使用了数形结合及分类讨论的数学方法和数学思想

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.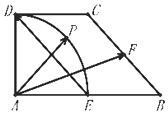 在直角梯形 ABCD 中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E,F 分别为
在直角梯形 ABCD 中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E,F 分别为
AB,AC 的中点,以A 为圆心,AD为半径的圆弧DE中点为P (如图所示).
若$\overrightarrow{AP}=λ\overrightarrow{ED}+μ\overrightarrow{AF}$,其中λ,μ∈R,则λ+μ的值是( )
 在直角梯形 ABCD 中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E,F 分别为
在直角梯形 ABCD 中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E,F 分别为AB,AC 的中点,以A 为圆心,AD为半径的圆弧DE中点为P (如图所示).
若$\overrightarrow{AP}=λ\overrightarrow{ED}+μ\overrightarrow{AF}$,其中λ,μ∈R,则λ+μ的值是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{3\sqrt{2}}}{4}$ | C. | $\sqrt{2}$ | D. | $\frac{3}{4}$ |
9.若直线(a-1)x-2y+1=0与直线x-ay+1=0平行,则a=( )
| A. | -1或2 | B. | -1 | C. | 2 | D. | $\frac{1}{3}$ |
3.如图1是遂宁市某校高中学生身高的条形统计图,从左到右的各条形表示的学生人数依次记为A1,A2,…,A10(如A2表示身高(单位:cm)[150,155)内的学生人数).图2是图1中身高在一定分为内学生人数的一个算法流程图.现要统计身高在160~175cm(含160cm,不含175cm)的学生人数,那么在流程图中的判断框内应填入的条件是( )
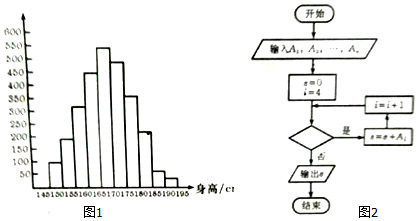

| A. | i<6 | B. | i<7 | C. | i<8 | D. | i<9 |
10.如果直线l将圆x2+y2+2x-4y=0平分,且不过第一象限,那么l的斜率的取值范围是( )
| A. | [0,2] | B. | (0,2) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,-2] |
7.已知△ABC满足∠BAC=60°,BC=2,对于△ABC外接圆上一点D,满足∠BCD=45°,则BD=( )
| A. | $\sqrt{6}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
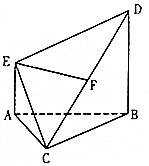 如图,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2,F为CD中点.
如图,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2,F为CD中点.