题目内容
20.$f(x)=\left\{{\begin{array}{l}{{2^x},x≤1}\\{{{log}_9}^x,x>1}\end{array}}\right.$,则$f(x)>\frac{1}{2}$的解集是(-1,1]∪(3,+∞).分析 根据指数函数的图象和性质,分析偶函数f(x)的单调性,结合f(x-1)<f(2),可得|x-1|<2,解得答案.
解答 解:当x≤1时,f(x)=2x为增函数,$f(x)>\frac{1}{2}$,
可得:2x$>\frac{1}{2}$,可得1≥x>-1;
故当x>1时,f(x)=log9x,
$f(x)>\frac{1}{2}$,
可得:log9x$>\frac{1}{2}$,可得x>3;
解得:x∈(3,+∞),
故答案为:(-1,1]∪(3,+∞).
点评 本题考查的知识点是分段函数的应用,指数函数的单调性,是函数图象和性质的综合应用,难度中档.

练习册系列答案
相关题目
11.经过点A(-1,4)且在x轴上的截距为3的直线方程是( )
| A. | x+y+3=0 | B. | x-y+5=0 | C. | x+y-3=0 | D. | x+y-5=0 |
8.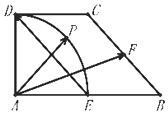 在直角梯形 ABCD 中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E,F 分别为
在直角梯形 ABCD 中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E,F 分别为
AB,AC 的中点,以A 为圆心,AD为半径的圆弧DE中点为P (如图所示).
若$\overrightarrow{AP}=λ\overrightarrow{ED}+μ\overrightarrow{AF}$,其中λ,μ∈R,则λ+μ的值是( )
 在直角梯形 ABCD 中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E,F 分别为
在直角梯形 ABCD 中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E,F 分别为AB,AC 的中点,以A 为圆心,AD为半径的圆弧DE中点为P (如图所示).
若$\overrightarrow{AP}=λ\overrightarrow{ED}+μ\overrightarrow{AF}$,其中λ,μ∈R,则λ+μ的值是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{3\sqrt{2}}}{4}$ | C. | $\sqrt{2}$ | D. | $\frac{3}{4}$ |
15.已知集合A={1,3,5},B={1,m},A∩B={1,m},则m等于( )
| A. | 1 或 3 | B. | 3 或 5 | C. | 1 或 5 | D. | 1 或 3 或5 |
12.在空间直角坐标系Oxyz中,z轴上的点M到点A(1,0,2)与点B(1,-3,1)的距离相等,则点M的坐标是( )
| A. | (0,0,-3) | B. | (0,0,3) | C. | (0,0,$\sqrt{10}$) | D. | (0,0,-$\sqrt{10}$) |
9.若直线(a-1)x-2y+1=0与直线x-ay+1=0平行,则a=( )
| A. | -1或2 | B. | -1 | C. | 2 | D. | $\frac{1}{3}$ |
10.如果直线l将圆x2+y2+2x-4y=0平分,且不过第一象限,那么l的斜率的取值范围是( )
| A. | [0,2] | B. | (0,2) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,-2] |
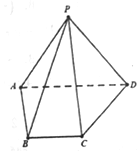 如图,三四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2.
如图,三四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2.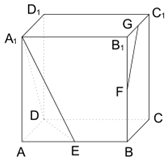 如 图,正方体ABCD-A1B1C1D1的棱长为2,E、F、G 分别为 AB、BB1、B1C1 的中点.
如 图,正方体ABCD-A1B1C1D1的棱长为2,E、F、G 分别为 AB、BB1、B1C1 的中点.