题目内容
19．将直线l沿y轴的负方向平移a（a＞0）个单位，再沿x轴正方向平移a+1个单位得直线l'，此时直线l'与l重合，则直线l'的斜率为（ ）| A． | $\frac{a}{a+1}$ | B． | -$\frac{a}{a+1}$ | C． | $\frac{a+1}{a}$ | D． | -$\frac{a+1}{a}$ |
分析 利用直线经过平移后，仍回到原来的位置时，设直线l上一点A（x，y），通过点的变化后仍在直线上，最后利用直线的斜率公式求解即可．
解答 解：设直线l上一点A（x，y），
其沿y轴负方向平移a个单位，再沿x轴正方向平移a+1个单位后的坐标为（x+a+1，y-a）
它仍然在直线l上，
∴直线l的斜率k=$\frac{y-a-y}{x+a+1-x}$=-$\frac{a}{a+1}$
故选：B．
点评 本小题主要考查函数的图象与图象变化等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
17．设随机变量X服从正态分布N（0，1），对给定的a（0＜a＜1），数ua由P（X＞ua）=α确定，若P（|X|＜x）=α，则x等于（ ）
| A． | u${\;}_{\frac{a}{2}}$ | B． | u${\;}_{1-\frac{a}{2}}$ | C． | u${\;}_{\frac{1-a}{2}}$ | D． | u1-a |
10．程序框图如图所示，其输出的结果为（ ）
| A． | 2100-1 | B． | 299-1 | C． | 2100 | D． | 299 |
7．等差数列{an}中Sn是其前n项和，a1=-2010，$\frac{{{S_{2011}}}}{2011}$-$\frac{{{S_{2009}}}}{2009}$=2，则S2010的值为（ ）
| A． | -2009 | B． | 2009 | C． | -2010 | D． | 2010 |
14．
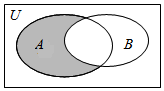设全集U=R，A={x|x（x-2）＜0}，B={x|y=$\sqrt{1-x}$}，则图中阴影部分表示的集合为（ ）
设全集U=R，A={x|x（x-2）＜0}，B={x|y=$\sqrt{1-x}$}，则图中阴影部分表示的集合为（ ）| A． | {x|0＜x≤1} | B． | {x|1＜x＜2} | C． | {x|x≤1} | D． | {x|1≤x＜2} |
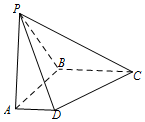如图，在底面是直角梯形的四棱锥P-ABCD中，∠DAB=90°，PA⊥平面ABCD，PA=AB=BC=3，梯形上底AD=1．