题目内容
4.已知向量|$\overrightarrow{a}$|=$\sqrt{5}$,$\overrightarrow{a}$•$\overrightarrow{b}$=10,|$\overrightarrow{a}$+$\overrightarrow{b}$|=5$\sqrt{2}$,则|$\overrightarrow{b}$|=( )| A. | $\sqrt{5}$ | B. | $\sqrt{10}$ | C. | 5 | D. | 25 |
分析 根据条件,对$|\overrightarrow{a}+\overrightarrow{b}|=5\sqrt{2}$两边平方,进行数量积运算即可求出${\overrightarrow{b}}^{2}$的值,从而得出$|\overrightarrow{b}|$的值.
解答 解:∵$|\overrightarrow{a}|=\sqrt{5},\overrightarrow{a}•\overrightarrow{b}=10$;
∴由$|\overrightarrow{a}+\overrightarrow{b}|=5\sqrt{2}$得,$(\overrightarrow{a}+\overrightarrow{b})^{2}={\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$=$5+20+{\overrightarrow{b}}^{2}=50$;
∴${\overrightarrow{b}}^{2}=25$;
∴$|\overrightarrow{b}|=5$.
故选:C.
点评 考查数量积的运算,以及要求$|\overrightarrow{b}|$而求${\overrightarrow{b}}^{2}$的方法.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
2.下列函数中,在区间(0,2)上为增函数的是( )
| A. | y=-2x+1 | B. | y=$\frac{1}{3}$x2+1 | C. | y=-x2-x-1 | D. | y=x2-x+1 |
19.将直线l沿y轴的负方向平移a(a>0)个单位,再沿x轴正方向平移a+1个单位得直线l',此时直线l'与l重合,则直线l'的斜率为( )
| A. | $\frac{a}{a+1}$ | B. | -$\frac{a}{a+1}$ | C. | $\frac{a+1}{a}$ | D. | -$\frac{a+1}{a}$ |
13.关于x的函数y=log${\;}_{\frac{1}{2}}$(x2-ax+2a)在[1,+∞)上为减函数,则实数a的取值范围是( )
| A. | (-∞,2] | B. | (-1,+∞) | C. | (-1,2] | D. | (-∞,-1) |
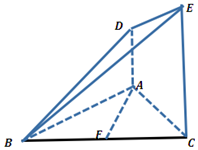 如图,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,四边形ACED的面积为$\frac{3}{2}$,F为BC的中点,
如图,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,四边形ACED的面积为$\frac{3}{2}$,F为BC的中点,