题目内容
10.设$\overrightarrow{a}$=(x,3),$\overrightarrow{b}$=(2,-1),根据下列条件求x的取值范围.(1)$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为锐角;
(2)$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为直角;
(3)$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为钝角.
分析 (1)由题意可得$\overrightarrow{a}$•$\overrightarrow{b}$=2x-3>0,且x×1-2×1≠0,解不等式求得 x 的取值范围;
(2)$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为直角,得数量积为0,求出x;
(3)由于$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为钝角,则$\overrightarrow{a}$•$\overrightarrow{b}$=2x-3<0,-x-6≠0,解出即可;
解答 解:(1)由题意可得$\overrightarrow{a}$•$\overrightarrow{b}$=2x-3>0,且-x+3×2≠0,∴x>$\frac{3}{2}$,且 x≠6,
故实数x的取值范围为 ($\frac{3}{2}$,+6)∪(6,+∞),
(2)$\overrightarrow{a}$,$\overrightarrow{b}$夹角为直角,所以$\overrightarrow{a}$•$\overrightarrow{b}$=2x-3=0,所以x=$\frac{3}{2}$;
(3)$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为钝角,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=2x-3<0,且-x+6≠0,
解得x<$\frac{3}{2}$.
点评 本题考查两个向量的数量积的定义,两个向量的数量积公式的应用,属于基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
20.下列说法中,正确的是( )
| A. | 命题“若x≠2或y≠7,则x+y≠9”的逆命题为真命题 | |
| B. | 命题“若x2=4,则x=2”的否命题是“若x2=4,则x≠2” | |
| C. | 命题“若x2<1,则-1<x<1”的逆否命题是“若x<-1或x>1,则x2>1” | |
| D. | 若命题p:?x∈R,x2-x+1>0,q:?x0∈(0,+∞),sinx0>1,则(¬p)∨q为真命题 |
1.已知二次函数y=f(x),当x=2时,函数f(x)取最小值-1,且f(1)+f(4)=3.
(1)求f(x)的解析式;
(2)若g(x)=f(x)-kx在区间(1,4)上无最小值,求实数k的取值范围.
(1)求f(x)的解析式;
(2)若g(x)=f(x)-kx在区间(1,4)上无最小值,求实数k的取值范围.
18.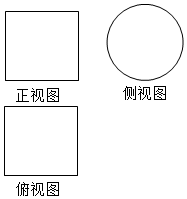 如图所示,一个空间几何体的正视图和俯视图都是边长为2的正方形,侧视图是一个直径为2的圆,则该几何体的表面积是( )
如图所示,一个空间几何体的正视图和俯视图都是边长为2的正方形,侧视图是一个直径为2的圆,则该几何体的表面积是( )
 如图所示,一个空间几何体的正视图和俯视图都是边长为2的正方形,侧视图是一个直径为2的圆,则该几何体的表面积是( )
如图所示,一个空间几何体的正视图和俯视图都是边长为2的正方形,侧视图是一个直径为2的圆,则该几何体的表面积是( )| A. | 4π | B. | 6π | C. | 8π | D. | 16π |
5.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 16-π | B. | 8+π | C. | 16+π | D. | 8-π |
15.已知F2,F1是双曲线 $\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的上、下焦点,点F2关于渐近线的对称点恰好落在以F1为圆心,|OF1|为半径的圆内,则双曲线的离心率e为( )
| A. | ($\sqrt{3}$,3) | B. | (3,+∞) | C. | ($\sqrt{2}$,2) | D. | (2,+∞) |
2.函数f(x)=|lgx|-sinx的零点个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |