题目内容
20.下列说法中,正确的是( )| A. | 命题“若x≠2或y≠7,则x+y≠9”的逆命题为真命题 | |
| B. | 命题“若x2=4,则x=2”的否命题是“若x2=4,则x≠2” | |
| C. | 命题“若x2<1,则-1<x<1”的逆否命题是“若x<-1或x>1,则x2>1” | |
| D. | 若命题p:?x∈R,x2-x+1>0,q:?x0∈(0,+∞),sinx0>1,则(¬p)∨q为真命题 |
分析 A.根据逆否命题的定义进行判断.
B.根据否命题的定义进行判断.
C.根据逆否命题的定义进行判断.
D.根据复合命题的真假关系进行判断.
解答 解:A.命题“若x≠2或y≠7,则x+y≠9”的否命题为,“若x=2且y=7,则x+y=9”,为真命题,则命题的逆命题为真命题正确,故A正确,
B.命题“若x2=4,则x=2”的否命题是“若x2≠4,则x≠2”,故B错误,
C.命题“若x2<1,则-1<x<1”的逆否命题是“若x≤-1或x≥1,则x2≥1”,故C错误,
D.∵x2-x+1=(x-$\frac{1}{2}$)2+$\frac{3}{4}$>0恒成立,∴命题p为真命题.,则¬p为假命题,
∵sinx∈[-1,1]?,∴?x0∈(0,+∞),sinx0>1为假命题.,则p是假命题,则(¬p)∨q为假命题.故D错误,
故选:A
点评 本题主要考查命题的真假判断,涉及四种命题的定义以及复合命题的真假关系,比较基础.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
10.下列命题中,假命题是( )
| A. | ?x∈N*,(x-2)2>0 | B. | ?x0∈R,tanx0=2 | C. | ?x0∈R,log2x0<2 | D. | ?x∈R,3x-2>0 |
8.若曲线f(x)=x3+x-2在点P0处的切线垂直于直线x+4y+3=0,则点P0的坐标为( )
| A. | (1,0) | B. | (2,8) | C. | (2,8)或(-1,-4) | D. | (1,0)或(-1,-4) |
15.△AOB为等边三角形,OA=1,OC为AB的高,点P在射线OC上,则$\overrightarrow{AP}•\overrightarrow{OP}$的最小值为( )
| A. | -$\frac{1}{4}$ | B. | -$\frac{1}{8}$ | C. | -$\frac{\sqrt{3}}{8}$ | D. | -$\frac{3}{16}$ |
12.已知|${\overrightarrow a}$|=1,|${\overrightarrow b$|=2$\sqrt{3}$,$\overrightarrow a$•(${\overrightarrow b$-$\overrightarrow a}$)=-4,则向量$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
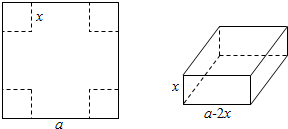 有一块边长为a的正方形铁板,现从铁板的四个角各截去一个相同的小正方形,做成一个长方体形的无盖容器,为使其容积最大,截下的小正方形边长应为多少?
有一块边长为a的正方形铁板,现从铁板的四个角各截去一个相同的小正方形,做成一个长方体形的无盖容器,为使其容积最大,截下的小正方形边长应为多少?