题目内容
12.已知函数f(x)=$\frac{2}{x}$+alnx-2,曲线y=f(x)在点P(1,f(1))处的切线与直线y=x+3垂直.(1)求实数a的值;
(2)记g(x)=f(x)+x-b(b∈R),若函数g(x)在区间[e-1,e]上有两个零点,求实数b的取值范围;
(3)若不等式πf(x)>($\frac{1}{π}$)1+x-lnx在|t|≤2时恒成立,求实数x的取值范围.
分析 (1)根据导数的几何意义,得 f′( 1)=-1,解得a,?
(2)g( x)=$\frac{2}{x}$+lnx+x-2-b( x>0),g′( x)=$\frac{{x}^{2}+x-2}{{x}^{2}}$,可得当 x=1 时,g( x) 取 得 极 小 值 g( 1);可得函 数 g( x) 在 区 间[e-1,e]上 有 两 个 零 点,$\left\{\begin{array}{l}{g(\frac{1}{e})≥0}\\{g(1)<0}\\{g(e)≥0}\end{array}\right.$⇒$\left\{\begin{array}{l}{2e+\frac{1}{e}-3-b≥0}\\{1-b<0}\\{\frac{2}{e}+e-1-b≥0}\end{array}\right.$,解得实数b的取值范围;
(3)π f(x)>($\frac{1}{π}$)t+x-lnx 在|t|≤2 时 恒 成 立,⇒f( x)>-t-x+lnx,即t+x2-2x+2>0 在|t|≤2 时 恒 成 立,令 g( t)=xt+x2-2x+2,x>0,只 需 g(-2)>0,即可
解答 解:(1)函 数 f( x) 的 定 义 域 为 ( 0,+∞),f′( x)=$\frac{-2}{{x}^{2}}+\frac{a}{x}$.
∵曲线y=f(x)在点P(1,f(1))处的切线与直线y=x+3垂直,
∴f′( 1)=-2+a=-1,解 得 a=1.?
(2)g( x)=$\frac{2}{x}$+lnx+x-2-b( x>0),g′( x)=$\frac{{x}^{2}+x-2}{{x}^{2}}$,
由 g′( x)>0,得 x>1,由 g′( x)<0,得 0<x<1?,
∴g( x) 的 单 调 递 增 区 间 是 ( 1,+∞),单 调 递 减 区 间 为 ( 0,1),
当 x=1 时,g( x) 取 得 极 小 值 g( 1),?
∵函 数 g( x) 在 区 间[e-1,e]上 有 两 个 零 点,∴$\left\{\begin{array}{l}{g(\frac{1}{e})≥0}\\{g(1)<0}\\{g(e)≥0}\end{array}\right.$
⇒$\left\{\begin{array}{l}{2e+\frac{1}{e}-3-b≥0}\\{1-b<0}\\{\frac{2}{e}+e-1-b≥0}\end{array}\right.$,解得1$<b≤\frac{2}{e}+e-1$,
∴b 的 取 值 范 围 是 ( 1,$\frac{2}{e}$+e-1];
(3)∵π f(x)>($\frac{1}{π}$)t+x-lnx 在|t|≤2 时 恒 成 立,∴f( x)>-t-x+lnx,
即xt+x2-2x+2>0 在|t|≤2 时 恒 成 立,令 g( t)=xt+x2-2x+2,(x>0),
∴只 需 g(-2)>0,即 x2-4x+2>0
解 得x∈( 0,2-$\sqrt{2}$)∪(2+$\sqrt{2}$,+∞)
点评 本题考查了导数的几何意义,利用导数求函数单调性、极值,考查了函数与方程思想、转化思想,属于中档题.

 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案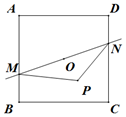 正方形ABCD边长为2,中心为O,直线l经过中心O,交AB于M,交CD于N,P为平面上一点,且$2\overrightarrow{OP}=λ\overrightarrow{OB}+(1-λ)\overrightarrow{OC}$,则$\overrightarrow{PM}•\overrightarrow{PN}$的最小值是( )
正方形ABCD边长为2,中心为O,直线l经过中心O,交AB于M,交CD于N,P为平面上一点,且$2\overrightarrow{OP}=λ\overrightarrow{OB}+(1-λ)\overrightarrow{OC}$,则$\overrightarrow{PM}•\overrightarrow{PN}$的最小值是( )| A. | $-\frac{3}{4}$ | B. | -1 | C. | $-\frac{7}{4}$ | D. | -2 |
| A. | $\frac{1}{10}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{10}$ |
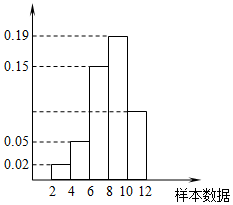 有一个容量为300的样本,其频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在区间[10,12)内的频数为( )
有一个容量为300的样本,其频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在区间[10,12)内的频数为( )| A. | 27 | B. | 81 | C. | 54 | D. | 108 |