题目内容
己知 定义在R上的函数,当x∈[0,2]时,f(x)=8(1-|x-1|),且对于任意的实数x∈[2n-2,2n+1-2](n∈N,且n≥2),都有f(x)=
f(
-1),若函数g(x)=f(x)-logax有且只有三个零点,则a的取值范围为 .
| 1 |
| 2 |
| x |
| 2 |
考点:分段函数的应用
专题:函数的性质及应用
分析:由g(x)=f(x)-logax=0,得f(x)=logax,分别作出函数f(x)和y=logax的图象,利用数形结合即可得到结论.
解答:
解:当x∈[0,2]时,f(x)=8(1-|x-1|),
当n=2时,x∈[2,6],此时
-1∈[0,2],则f(x)=
f(
-1)=
×8(1-|
-1-1|)=4(1-|
-2|),
当n=3时,x∈[6,14],此时
-1∈[2,6],则f(x)=
f(
-1)=
×4(1-|
-
|)=2(1-|
-
|),
由g(x)=f(x)-logax=0,得f(x)=logax,分别作出函数f(x)和y=logax的图象,
若0<a<1,则此时两个函数图象只有1个交点,不满足条件.
若a>1,当对数函数图象经过A时,两个图象只有2个交点,当图象经过点B时,两个函数有4个交点,
则要使两个函数有3个交点,则对数函数图象必须在A点以下,B点以上,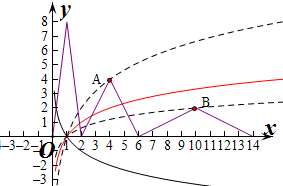
∵f(4)=4,f(10)=2,∴A(4,2),B(10,2),
即满足
,
即
,解得
,
即2<a2<10,
∵a>1,
∴
<a<
,
故则a的取值范围为是(
,
),
故答案为:(
,
)
当n=2时,x∈[2,6],此时
| x |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| x |
| 2 |
当n=3时,x∈[6,14],此时
| x |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
| x |
| 4 |
| 5 |
| 2 |
| x |
| 4 |
| 5 |
| 2 |
由g(x)=f(x)-logax=0,得f(x)=logax,分别作出函数f(x)和y=logax的图象,
若0<a<1,则此时两个函数图象只有1个交点,不满足条件.
若a>1,当对数函数图象经过A时,两个图象只有2个交点,当图象经过点B时,两个函数有4个交点,
则要使两个函数有3个交点,则对数函数图象必须在A点以下,B点以上,

∵f(4)=4,f(10)=2,∴A(4,2),B(10,2),
即满足
|
即
|
|
即2<a2<10,
∵a>1,
∴
| 2 |
| 10 |
故则a的取值范围为是(
| 2 |
| 10 |
故答案为:(
| 2 |
| 10 |
点评:本题主要考查分段函数的应用,利用函数零点和方程之间的关系,将条件转化为两个函数交点问题,利用数形结合是解决本题的关键.综合性较强,有一点的难度.

练习册系列答案
相关题目
设a>b>0,且ab=2,则a2+
的最小值是( )
| 1 |
| a(a-b) |
| A、1 | B、2 | C、3 | D、4 |
已知m和n是两条不同的直线,α和β是两个不重合的平面,则下列给出的条件中,一定能推出m⊥β的是( )
| A、α⊥β且m?α |
| B、α⊥β且m∥α |
| C、m∥n且n⊥β |
| D、m⊥n且n∥β; |
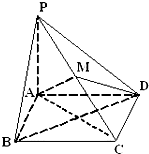 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,PA=1,点M是棱PC上的一点,且AM⊥PB.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,PA=1,点M是棱PC上的一点,且AM⊥PB.