题目内容
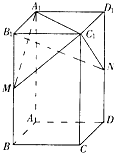 如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别是棱BB1,DD1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别是棱BB1,DD1的中点.(Ⅰ)求异面直线A1M与B1C所成的角的余弦值;
(Ⅱ)求证:平面A1MC1⊥平面B1NC1.
考点:平面与平面垂直的判定,异面直线及其所成的角
专题:空间位置关系与距离
分析:(Ⅰ)由A1D∥B1C,又MA1=
,A1D=
,MD=
,可得cos∠MA1D=
.
(Ⅱ)取AA1的中点P,联结B1P,NP,MP,则B1P∥C1N,可得A1M⊥B1P,A1M⊥C1N,又B1C1⊥平面A1B,A1M?平面A1B,可得A1M⊥平面B1NC1.从而可证平面A1MC1⊥平面B1NC1.
| 2 |
| 5 |
| 3 |
| ||
| 5 |
(Ⅱ)取AA1的中点P,联结B1P,NP,MP,则B1P∥C1N,可得A1M⊥B1P,A1M⊥C1N,又B1C1⊥平面A1B,A1M?平面A1B,可得A1M⊥平面B1NC1.从而可证平面A1MC1⊥平面B1NC1.
解答:
解:(Ⅰ)∵A1D∥B1C,∴∠MA1D是异面直线A1M与B1C所成的角(或补角).
又MA1=
,A1D=
,MD=
,
∴cos∠MA1D=
.
∴A1M与B1C所成的角的余弦值为
…(4分)
(Ⅱ)取AA1的中点P,联结B1P,NP,MP,则B1PNC1为平行四边形,∴B1P∥C1N
又A1B1MP1为正方形,∴A1M⊥B1P,∴A1M⊥C1N,
又B1C1⊥平面A1B,A1M?平面A1B,∴B1C1⊥A1M,
∴A1M⊥平面B1NC1.
又A1M?平面A1MC1,∴平面A1MC1⊥平面B1NC1.…(8分)
(注意:若用向量法相应给分)
又MA1=
| 2 |
| 5 |
| 3 |
∴cos∠MA1D=
| ||
| 5 |
∴A1M与B1C所成的角的余弦值为
| ||
| 5 |
(Ⅱ)取AA1的中点P,联结B1P,NP,MP,则B1PNC1为平行四边形,∴B1P∥C1N
又A1B1MP1为正方形,∴A1M⊥B1P,∴A1M⊥C1N,
又B1C1⊥平面A1B,A1M?平面A1B,∴B1C1⊥A1M,
∴A1M⊥平面B1NC1.
又A1M?平面A1MC1,∴平面A1MC1⊥平面B1NC1.…(8分)
(注意:若用向量法相应给分)
点评:本题主要考查了异面直线及其所成的角,平面与平面垂直的判定,属于基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
与圆x2+y2=1以及x2+y2-8x+12=0都外切的圆的圆心在( )
| A、一个椭圆 |
| B、双曲线的一支上 |
| C、一条抛物线上 |
| D、一个圆上 |
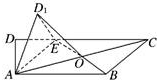 如图,在梯形ABCD中,AB∥CD,∠ADC=90°,AB=2,DC=3,AD=1.E是DC上一点,且DE=1,连接AE,将△DAE沿AE折起到△D1AE的位置,使得∠D1AB=30°,设AC与BE的交点为O.
如图,在梯形ABCD中,AB∥CD,∠ADC=90°,AB=2,DC=3,AD=1.E是DC上一点,且DE=1,连接AE,将△DAE沿AE折起到△D1AE的位置,使得∠D1AB=30°,设AC与BE的交点为O.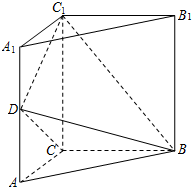 如图,三棱柱ABC-A1B1C1中,侧棱垂直于底面,∠ACB=90°,AC=BC=
如图,三棱柱ABC-A1B1C1中,侧棱垂直于底面,∠ACB=90°,AC=BC=