题目内容
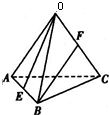
在四面体OABC中,各棱长都相等,E、F分别为AB,OC的中点,求异面直线OE与BF所夹角得余弦值.
考点:异面直线及其所成的角
专题:空间角
分析:利用向量法即可求出异面直线OE与BF所成角的余弦值.
解答:
解:设
=
,
=
,
=
,且|
|=|
|=|
|=1,
则∠AOB=∠BOC=∠AOC=
,
则
•
=
•
=
•
=
,
=
(
+
),
=
-
=
-
=
-
,
|
|=|
|=
,
则
•
=
(
+
)•(
-
)=
•
+
•
-
•
-
2=-
,
∴cos<
,
>=
=
=-
,
故异面直线OE与BF所夹角得余弦值为
.
| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
则∠AOB=∠BOC=∠AOC=
| π |
| 3 |
则
| a |
| b |
| c |
| a |
| b |
| c |
| 1 |
| 2 |
| OE |
| 1 |
| 2 |
| a |
| b |
| BF |
| OF |
| OB |
| 1 |
| 2 |
| OC |
| OB |
| 1 |
| 2 |
| c |
| b |

|
| OE |
| BF |
| ||
| 2 |
则
| OE |
| BF |
| 1 |
| 2 |
| a |
| b |
| 1 |
| 2 |
| c |
| b |
| 1 |
| 4 |
| c |
| a |
| 1 |
| 4 |
| b |
| c |
| 1 |
| 2 |
| a |
| b |
| 1 |
| 2 |
| b |
| 1 |
| 2 |
∴cos<
| OE |
| BF |
| ||||
|
|
-
| ||||||||
|
| 2 |
| 3 |
故异面直线OE与BF所夹角得余弦值为
| 2 |
| 3 |
点评:本题主要考查异面直线所成角的求解,利用向量法是解决本题的关键.

练习册系列答案
相关题目
圆柱的轴截面ABCD是边长为2的正方形,M为正方形ABCD的对角线的交点,动点P在圆柱下底面内(包括圆周),若直线AM与直线MP所成的角为45°,则点P形成的轨迹为( )
| A、椭圆的一部分 |
| B、抛物线的一部分 |
| C、双曲线的一部分 |
| D、圆的一部分 |
若双曲线x2-y2=a2(a>0)的左、右顶点分别为A、B,点P是第一象限内双曲线上的点.记∠PAB=α,且∠PBA=β,则( )
A、α+β=
| ||
B、β-α=
| ||
| C、β=2α | ||
| D、β=3α |
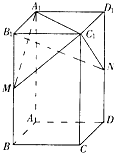 如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别是棱BB1,DD1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别是棱BB1,DD1的中点.