题目内容
已知sin(x-2π)-cos(π-x)=
,x为第二象限角,求:
(1)sinx与cosx的值;
(2)角x的集合.
1-
| ||
| 2 |
(1)sinx与cosx的值;
(2)角x的集合.
考点:同角三角函数基本关系的运用
专题:计算题,三角函数的求值
分析:(1)化简已知可得cosx=
-sinx,代入cos2x+sin2x=1中,可解得:cosx=-
或者 1,由x在第二象限,可得cosx=-
,从而可求sinx=
.
(2)由sinx=
.x在第二象限,可求得:x={x|x=2kπ+
,k∈Z}.
1-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
(2)由sinx=
| 1 |
| 2 |
| 2π |
| 3 |
解答:
解:(1)∵sin(x-2π)-cos(π-x)=sinx+cosx=
,
∴cosx=
-sinx,
代入cos2x+sin2x=1中,
整理得方程:
4cos2x-2(1-
)cosx-
=0,
解得:cosx=-
或者 1,
∵x在第二象限,
∴cosx<0,取cosx=-
,
∴sinx=
-(-
)=
.
(2)∵sinx=
.x在第二象限,
∴可求得:x={x|x=2kπ+
,k∈Z}.
1-
| ||
| 2 |
∴cosx=
1-
| ||
| 2 |
代入cos2x+sin2x=1中,
整理得方程:
4cos2x-2(1-
| 3 |
| 3 |
解得:cosx=-
| ||
| 2 |
∵x在第二象限,
∴cosx<0,取cosx=-
| ||
| 2 |
∴sinx=
1-
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
(2)∵sinx=
| 1 |
| 2 |
∴可求得:x={x|x=2kπ+
| 2π |
| 3 |
点评:本题主要考查了同角三角函数基本关系的运用,属于基本知识的考查.

练习册系列答案
相关题目
已知A,B,C为△ABC的三个内角,所对的边分别为a,b,c,且bcosA=acosB,则下列结论正确的是( )
| A、A>C | B、A<B |
| C、A>B | D、A=B |
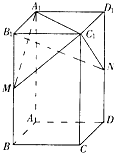 如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别是棱BB1,DD1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别是棱BB1,DD1的中点.